Complex Analysis: #4 Cauchy`s Theorem (simplest version)
Theorem 1
Let G ⊂ ℂ be a region, and assume that the function f : G → ℂ has an antiderivative (auf deutsch: Stammfunktion) F : G → ℂ with F' = f. Let γ be a closed path in G (that is, a continuous, closed, piecewise continuously differentiable path). (Closed means that γ(t0) = γ(t1).) Then ∫γ f(z)dz = 0.
Proof
Since every polynomial has an antiderivative, it follows that the path integral around a closed path for any polynomial is zero.
Of course this is all a bit too trivial. So let’s call the following theorem the simplest version of Cauchy’s integral theorem.
Theorem 2
Let Q be a (solid) triangle in the complex plane. Assume that Q ⊂ G ⊂ ℂ, and take f : G → ℂ to be an analytic function. Let γ be the closed path traveling around the three sides of Q. Then ∫γ f(z)dz = 0.
Proof
We may assume that γ begins and ends in a corner of Q — for example the “lowest” corner γ in the complex plane. If the lower side of Q is parallel to the real number axis, then take the right-hand corner on that side. Let us now divide the sides of Q in half, connecting the half-way points with straight line segments, thus creating four equal sub-triangles, Q1, . . . , Q4. Let γj be the path traveling around the boundary of Qj, for j = 1, . . . , 4. Again we may assume that each γj begins and ends in the bottom right corner of it’s triangle. So we have
Assume further that each of these paths is parameterized in the simplest way possible, so that |γ'| = 1 and |γj'| = 1 for all the j. Therefore Lγ is the sum of the lengths of the three sides of the triangle Q, and Lγj = Lγ/2 for each of the j.
Let’s say that γ1 is one of the numbers between one and four such that the value of
is the greatest. Then we certainly have
The next step is to concentrate on the triangle Qj1. As with Q, we subdivide Qj1 into four equal sub-triangles and we take paths around their boundaries. Choose Qj2 to be one of these sub-triangles of Qj1 which is such that the value of
is the greatest. Here γj2 is the path around the boundary of Qj2. Now we have Lγj2= Lγ/4, and
This whole process is continued indefinitely, so that we obtain a sequence of triangles, becoming smaller and smaller, converging to a point, z0 ∈ Q say,
Q ⊃ Qj1⊃
Qj2
⊃ · · · → z0
∈ Q.
For each n we have Lγjn= Lγ/2n and
But we have assumed that f is analytic, in particular it is differentiable at the point z0. Thus we can write
f(z) = f(z0) + f '(z0)(z − z0) + χ(z),
for points z in G, where χ : G → ℂ is a continuous function with
So let ∈ > 0 be arbitrarily given. Then there exists some δ > 0 such that |χ(z)| < |z − z0| for all z with 0 < |z − z0| < δ.
Now we need only choose n so large that |z − z0| < δ for all z ∈ Qjn. For such z we have
On the other hand, again since the length of Lγjnis Lγ/2n, we have
Bearing in mind Theorem 1 (and remembering that f '(z0) is simply a constant complex number), we conclude that
Since ∈ was arbitrary and Lγ remains constant, we conclude that ∫γ f(z)dz = 0.
But now Theorem 2 can be turned around, and we obtain (almost) the converse.
Theorem 3
Assume G ⊂ ℂ is a region and f : G → ℂ is a continuous function. Assume furthermore that for any solid triangle Q contained in G we have ∫γ f(z)dz = 0, where γ is the path around the triangle. Then f has an antiderivative in every open disc contained in G. That is, let U = {z ∈ ℂ : |z − z*| < r} be some such disc, where z* is a complex number (the middle point of the disc) and r > 0 is the radius of the disc. Then there exists F : U → ℂ with F'(z) = f(z) for all z ∈ U.
Proof
By replacing f with the function f*, where f*(z) = f(z − z*), we obtain the situation that z* = 0. Clearly, if the theorem is true for f*, then it is also true for f. Therefore, without loss of generality, we may simply assume that z* = 0.
Within U the function F is defined to be
Here, αz is the straight line from 0 to z, that is, αz(t) = tz. To show that F really is an antiderivative to f in U, let z0 be some arbitrary point of U and let z be some other point of U. Let β be the straight line connecting z0 to z. That is, β(t) = (1 − t)z0 + tz. Being a triangle, the integral of f around the path from 0 out to z, then from z to z0 then from z0 back to 0 must itself be zero. That is,
Looking at the definition of the path integral, we see that
Combining this theorem with Theorems 1 and 2, we see that if D ⊂ G is a closed disc, and γ is the circle of it’s boundary, then ∫γ f(z)dz = 0, for any analytic function defined in the region G. In fact, if γ is any (piecewise continuously differentiable and continuous) closed path contained within this disc-like G, then ∫γ f(z)dz = 0. For example we can look at a rectangle [a, b] × [c, d] contained within G. Since the rectangle can be taken to be a union of two triangles, attached along one side, we see that also the path integral around the rectangle must be zero.
More generally, the following theorem will prove to be useful.
Theorem 4
Let Q = {x + iy : 0 ≤ x, y ≤ 1} be the standard unit square in ℂ. Take ζ to be the standard closed path, traveling around the boundary of Q once in a counterclockwise direction, beginning and ending at 0. Assume that a continuously differentiable mapping ϕ : Q → ℂ is given, such that ϕ(Q) ⊂ G, a region where an analytic function f : G → ℂ is defined. Let γ = ϕ ◦ ζ be the image of ζ under ϕ. Then ∫γ f(z)dz = 0.
Proof.
Since Q is compact, ϕ(Q) is also compact. Therefore it can be covered by a finite number of γ open discs in G. But Q can now be partitioned into a finite number of sub-squares Q1, . . ., Qn such that ϕ(Qj) is in each case contained in a single one of these open discs. The theorem then follows by observing that the path integral around each of these sub-square images must be zero.
Note:-
[The inverse images of the open discs in Q form a finite open covering V1, . . ., Vm of Q. A sequence of partitions of Q can be obtained by cutting it along horizontal and vertical lines spaced 1/n apart, for each n ∈ ℕ. Can it be that for each of these partitions, there exists a sub-square which is not contained completely in one of the open sets Vk? But that would mean that there exists a limit point q ∈ Q such that for every ∈ > 0, there are infinitely many of these sub-squares contained within a distance of from q. However q ∈ Vk, for some k, and since Vk is open, there exists an ∈-neighborhood of q contained entirely within Vk, providing us with the necessary contradiction.]
A special case is the following.
Theorem 5
Let D1 and D2 be closed discs in ℂ such that D2 is contained in the interior of D1. Let γj be the closed path going once, counterclockwise, around the boundary of Dj, j = 1, 2. Let G ⊂ ℂ be a region containing D1\D2 and also containing the boundary of D2. Assume that f : G → ℂ is analytic. Then ∫γ1 f(z)dz = ∫γ2 f(z)dz.
Proof
The annulus between D2 and D1 can be taken to be the image of the unit square under a continuously differentiable mapping.
A convenient notation for this situation is the following. Let γ : [0, 1] → ℂ be the path γ(t) = z0 + re2πit . Then we simply write
With this notation, we can say that if the analytic function f is defined in a region containing the annulus {z ∈ ℂ : r ≤ |z| ≤ R}, then we must have

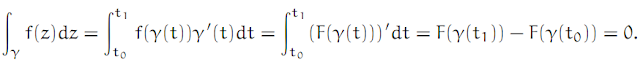









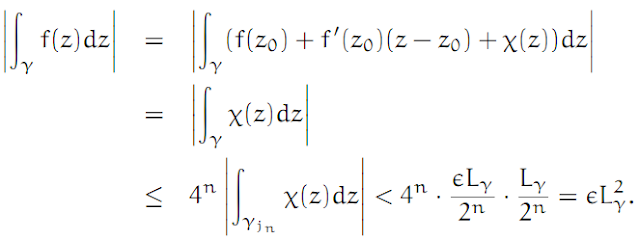





No comments:
Post a Comment
If it's a past exam question, do not include links to the paper. Only the reference.
Comments will only be published after moderation