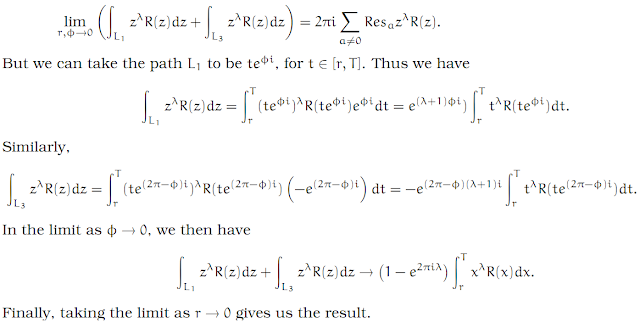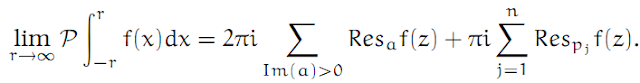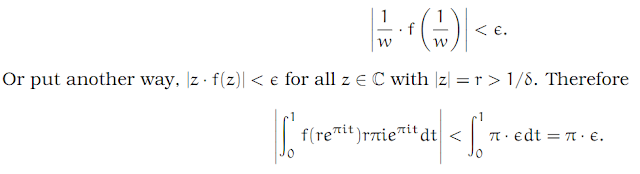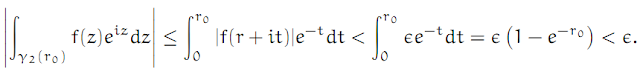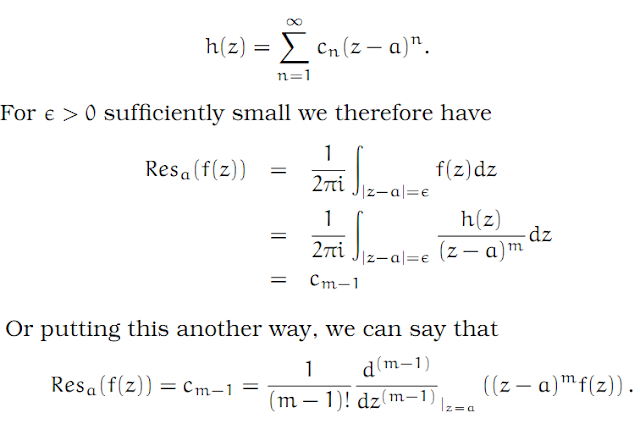• Complex Analysis: #19 Integrating Out From a Pole

Maybe we are dissatisfied with this “Cauchy principle value” technique. After all, it is rather like cheating! So let’s see what we can do with an integral like

where 0 is a pole, and ∞ is a zero of f. For example, look at the function f(x) = 1/x. But here we see big problems! Both of the integrals ∫₁^∞ f(x)dx and  ∫₀¹ f(x)dx are divergent.

Thinking about this, we see that the problems with the function 1/x stem from the fact that, first of all, the zero at ∞ is simple, and second of all, the pole at 0 is simple. This leads us to formulate the following theorem.


Theorem 39
Again, let R be a rational function defined throughout ℂ, but this time with a zero of order at least 2 at ∞. Furthermore, R has no poles in the positive real numbers (x > 0), and at most a simple pole at 0. Then we have

for all 0 < λ < 1.

Proof
As before, the function z^λR(z) has at most finitely many poles in ℂ. Let γ_{r, φ}, where 0 < r < 1 and 0 < φ < π, be the following closed curve. It starts at the point re^φi and follows a straight line out to the point Te^φi, where T = 1/r. Next it travels counter-clockwise around the circle of radius T, centered at 0, till it reaches the point Te^(2π−φ)i. Next it travels along a straight line to the point re^(2π−φ)i. Finally it travels back to the starting point, following the circle of radius r in a clockwise direction. Lets call these segments of the path L₁, L₂, L₃ and L₄. By choosing r and φ to be sufficiently small, we ensure that the path γ_{r, φ} encloses all poles of the function. In the exercises, we have seen that the path integrals along the segments L₂ and L₄ tend to zero for r → 0. Thus we have

• Complex Analysis: #18 Integrating across a Pole

For example, consider the "integral"

Obviously this is nonsense, since the integrals from −1 to 0, and from 0 to 1 of the function 1/x diverge. Specifically, for 0 < ∈ < 1 we have

Thus, if we agree to abandon the principles we have learned in the analysis lectures, and simply say that

then we have the Cauchy principle value of the integral, and we see that in this case it is simply zero. One could make an important-looking definition here, but let us confine our attention to integrals along closed intervals [a, b] ⊂ ℝ of complex-valued functions, where there might be poles of the function in the given interval. Assume for the moment there is a single pole at the point p ∈ (a, b). Then we will define the principle value of the integral (if it exists) to be

Then the generalization to having a finite number of poles of f along the interval (but not at the endpoints) is clear.


Theorem 38
Let R be a rational function, defined throughout ℂ (together with it’s poles). Assume that it has a zero at infinity, so that there can only be finitely many poles. Let p₁ < . . .  < p_m be the poles of R which happen to lie on ℝ. Assume that each of these poles is simple; that is, of order 1. We distinguish two cases:

• If R has a simple zero at infinity (that is, of order 1), then we take f(z) = R(z)e^iz. 
• Otherwise, R has a pole of order at least 2 at infinity, and in this case we take f(z) = R(z). 

Then we have

Proof
In either case, we can have only finitely many poles of the function f; therefore only finitely many poles along the real number line. Let γ_δ be the path along the real number line from −∞ to ∞, but altered slightly, following a semi-circle of radius δ above each of the poles on the real line. Furthermore, δ is sufficiently small that no other pole of f is enclosed within any of the semi-circles. Then, according to our previous theorems, we have

To simplify our thoughts, let us first consider the case that there is only one single pole p ∈ ℝ on the real number line. And to simplify our thoughts even further, assume that p = 0. Then we have the path γ_δ coming from −∞ to −δ, then it follows the path δe^iπ(1−t), for t going from 0 to 1, and then finally it goes straight along the real number line from δ to ∞.

Let us now consider the Laurent series around 0. We can write

say. But then we can just define the new function g throughout ℂ (leaving out the finite set of poles of f) by the rule

Obviously g has no pole at 0, but otherwise it has the same set of poles as the original function f. Since the function c₋₁/z is analytic at all these other poles, the residue of g is identical with that of f around each of these poles. Therefore

Now, to get the principle value of the integral for f, we use the path γ_δ, but we must remove the semi-circle part of it. That is, let

• Complex Analysis: #17 Residues Around the Point at "Infinity"

In many applications, one speaks of the properties of a function “at infinity”. For this, we take the “compactification” of the complex number plane. This is the set ℂ ∪ {∞}, where “∞” is simply an abstract symbol. Then the open sets of ℂ ∪ {∞} are, first of all the familiar open sets of ℂ, then in addition, we say that any set of the form {z ∈ ℂ : |z| > R} ∪ {∞} is open, for R > 0. Finally, the union of all these sets of sets gives the topology of ℂ ∪ {∞}. It turns out that ℂ ∪ {∞} is homeomorphic to the standard 2-sphere. It is often called the “Riemann sphere”.

Definition 13
Let G ⊂ ℂ ∪ {∞} be a region containing ∞. (Thus G is open and connected.) [Note that we must then have ℂ \ G being a closed and bounded set, thus compact.] We will say that f : G → ℂ is analytic at ∞ if the function given by f(1/z) has a removable singularity at 0. Similarly, f has a zero of order n, or a pole of order n at ∞ if the respective property is true of the function f(1/z) at 0. That is to say, if ∞ is a zero of order n of f then we would like to have the function wⁿf(w) having a removable, non-zero singularity at ∞. However this is the same as looking at the limit as z → 0 of the function which is given by substituting w = 1/z. That is, the function

So f has a zero of order n at infinity if g has a removable, non-zero singularity at 0.


Theorem 36
Let g, h : ℂ → ℂ be entire, not constant, functions (thus they are analytic at all points of ℂ). Let f be the meromorphic function f = g/h. Assume that there is no zero of h on the real number line. Assume furthermore that f has a zero at infinity of order at least 2. Then we have

(Here the sum is over all poles of the function f in the “upper” half plane of ℂ. That is, the set of all complex numbers with positive imaginary parts.)

Proof
Because f has a zero at infinity, we have f being bounded outside of a compact disc of the form D = {z ∈ ℂ : |z| ≥ r}, for some sufficiently large r > 0. In particular, all of the poles of f must be within D. Since the zeros of h are isolated, there are only finitely many of them, thus the sum over the poles is finite. Therefore, the residue theorem shows that

where γ is the closed curve which consists of two segments: first the segment along the real number line from −r to r, then the segment consisting of the semi-circle of radius r around zero, traveling upwards from r and around through ir, then coming back to −r. That is to say,

We are assuming that f has a zero at infinity of order at least 2. That means, for all ∈ > 0 there exists some δ > 0 such that for all w ≠ 0 in ℂ with |w| < δ, we have

Since ∈ can be taken to be arbitrarily small, giving a corresponding δ, we can choose our r to be greater than 1/δ, and thus the integral around the half-circle α_r is small. The limit r → ∞ gives the formula of the theorem.

So this gives a method of calculating an integral along the real number line without actually having to do the integral at all! We only need to know the residues of the poles of the function in the upper half-plane of ℂ; no poles are allowed to be on the real number line; and the function should tend to zero sufficiently quickly at infinity.

But the assumption that the zero at infinity is of order 2 or more might be too restrictive. Perhaps the function we happen to be looking at only has a simple zero at infinity. For example consider the function

The integral along the real number line does not converge, and so this shows that we cannot expect the integral to exist if the zero at infinity is only of the first order. But perhaps the following theorem, where f(x) is multiplied with the “rotating” function e^ix, thus mixing things up nicely, might be useful. However, in contrast to the case where the zero at infinity is of at least second order, here we cannot expect that the integral over the absolute value of the function also converges.


Theorem 37
The same assumptions as in the previous theorem, except that the zero of f at infinity is only of the first order. Then we have

Proof
Again, we only have finitely many singularities in the upper half-plane. This time take a closed path γ consisting of four straight segments. The first segment is the straight line from the point −r to +r, along the real number line. The second segment goes from r to r + ir. The third from r + ir to −r + ir, and the fourth from −r + ir back to the starting point at −r. Let’s call these segments γ₁(r), . . . , γ₄(r). Following the ideas in the proof of the previous theorem, we see that it is only necessary to show that

for j = 2, 3, 4. Our assumption implies that for all ∈ > 0 there exists an r₀ > 0 such that |f(z)| < ∈ for all z with |z| > r₀. We will show that the absolute value of the integral along the path γ₂(r₀) is less than ∈ . The calculation for the other paths is similar. We have

Complex Analysis: #16 Residues Calculus

• Complex Analysis: #16 The Calculus of Residues

Let’s begin by thinking about a function f with a pole of order m at the point a ∈ ℂ. That is, in a sufficiently small neighborhood of a we can write h(z) = f(z)(z−a)^m, and after filling in the removable singularity of h at a, we have h(a) ≠ 0. Let

So this is a formula for the residue of a function with a pole at a.

A rather special case is the following. Let us assume that G ⊂ ℂ is a region, and g, h are both analytic functions defined on G. Assume that a ∈ G is a simple zero of h. (That is h(a) = 0, but h'(a) ≠ 0.) Assume furthermore that g(a) ≠ 0. Then let f = g/h. (Note that a function such as f, which is defined to be the ratio of two analytic functions, is called a rational function.) Therefore f is meromorphic in G. What is the residue of f at a? Writing g and h as power series around a, we have

Of course, going in the other direction, if a is a zero of g and h(a) ≠ 0, then the residue of f at a is simply zero. This is trivial.


Theorem 35 (The Residue Theorem)
Let the function f be defined and analytic throughout the region G ⊂ ℂ, except perhaps for a set S ⊂ G of isolated, not removable singularities. Let Ω be a cycle in G which avoids all these singularities and which is such that the winding number of Ω around all points of the compliment of G is zero. Then only finitely many points of S have non-vanishing index with respect to Ω and we have the residue formula

Proof
Nothing is lost if we assume that Ω simply consists of a single closed path γ. So it is contained in a compact disc in ℂ which must contain all points of ℂ having a non-vanishing index with respect to γ. If there were infinitely many such points, then they must have an accumulation point, which must lie in the compliment of G. But such a point has index zero with respect to γ. Since that point does not lie on γ, it must have a neighborhood which contains only points with index zero with respect to γ. Thus we have a contradiction. The residue theorem now follows from Cauchy’s theorem (theorem 26).

Complex Analysis: #15 Laurent Series

• Complex Analysis: #15 The Laurent Series

Since a pole of order n involves a function which looks somewhat like (z − z₀)⁻ⁿ, at least near to the singularity z₀, it seems reasonable to expand our idea of power series into the negative direction. This gives us the Laurent series. That is, a sum which looks like this:

There is a little problem with this notation. After all, if the series is not absolutely convergent, then we might get different sums if we start at different places in the doubly infinite sequence. Let us therefore say that the sum from 0 to +∞ is the positive series, and that from −∞ to −1 is the negative series. So the whole series is absolutely convergent if both the positive and negative series are absolutely convergent. [The negative series is called the “Hauptteil” in German, whilst the positive series is the “Nebenteil”.] One can obviously imagine that the negative series is really a positive series in the variable 1/(z − z₀).

So given some collection of coefficients c_n for all n ∈ ℤ, let R ≥ 0 be the radius of convergence of the series

That is to say, if 1/|z − z₀| < 1/r, or put another way, if |z − z₀| > r, then the negative series

converges.

Therefore, there is an open ring (or annulus) of points of the complex plane, namely the region {z ∈ ℂ : r < |z − z₀| < R}, where the Laurent series is absolutely convergent. In this ring, the function defined by the Laurent series

is analytic. Note however that it is not necessarily true that f has an antiderivative. We see this by observing that the particular term c₋₁(z − z₀)⁻¹ has no antiderivative in the ring. On the other hand, if we happen to have c₋₁ = 0 then there is an antiderivative, namely the function in the ring given by the Laurent series

Theorem 29
Assume the Laurent series converges in the ring between 0 ≤ r < R ≤ ∞. Let r < ρ < R. The coefficients of the Laurent series are then given by

Proof
Since the series is uniformly convergent around the circle of radius ρ, we can exchange sum and integral signs to write

However, if we look at the individual terms, we see that if k ≠ n, then each term has an antiderivative,
and thus the path-integral is zero for that term. We are left with the n-term, and this is then simply

Conversely, we have:


Theorem 30
Given 0 ≤ r < ρ ≤ R, let G = {z ∈ ℂ : r < |z − z₀| < R} and f : G → ℂ be an analytic function. Then we have f(z) = ∑ c_nzⁿ, (with n = −∞, . . ., ∞) , where

Proof
For simplicity, choose z₀ = 0. Let z be given with r < |z| < R, and take ∈ > 0 such that ∈ < min{R − |z|, |z| − r}. Thus, according to theorems 5 and 6, we have

(Note that theorem 5 shows that the integrals for |z| = R − ∈, and for |z| = r + ∈ are equal to the integrals, taken along the path |z| = ρ.)


Theorem 31
Again, the same assumptions as in theorem 30. Assume further that there exists some M > 0 with |f(z)| ≤ M for all z with |z − z₀| = ρ. Then |c_n| ≤ M/ρⁿ for all n.

Proof

Theorem 32 (Riemann)
Let a ∈ G ⊂ ℂ be an isolated singularity of an analytic function f : G\{a} → ℂ such that the exists an M > 0 and an ∈ > 0 with |f(z)| ≤ M for all z₀ ∈ G with z ≠ a and |z − a| < ∈ . Then a is a removable singularity.

Proof
For then |c_n| ≤ M/rⁿ for all 0 < r < ∈ , and therefore, for the terms with n < 0 we must have c_n = 0, showing that in fact f is given by a normal power series, and thus it is also analytic in a.


Theorem 33 (Casorati-Weierstrass)
Let a be an essential singularity of the function f : G \ {a} → ℂ. Then for all ∈ , δ > 0 and w ∈ ℂ, there exists a z ∈ G with |z − a| < ∈ such that |f(z) − w| < δ. (Which is to say, arbitrarily small neighborhoods of a are “exploded” through the action of f throughout ℂ, so that they form a dense subset of ℂ!)

Proof
Otherwise, there must exist some w₀ ∈ ℂ such that there exists an ∈ > 0 and |f(z) −w₀| ≥ δ for all z ∈ G with |z − a| < ∈ . Let B(a, ∈) = {z ∈ ℂ : |z − a| < ∈ } and define the function h : (B(a, ∈ )\{a})∩G → ℂ to be

Clearly h is analytic, with an isolated singularity at the point a. Furthermore.

Therefore, according to theorem 32 we must have a being removable. Thus, writing

we see that since the function given by 1/h(z) has at most a pole at a, we cannot have a being an essential singularity of f. This is a contradiction.

As an example of a function with an essential singularity, consider the function f(z) = exp(1/z). Clearly f is defined for all z ≠ 0, and not defined for the single point 0. In fact, 0 is an essential singularity. To see this, consider the exponential series

The singularity at 0 obviously cannot be a pole of the function, since the negative series is infinite. In fact we can make a theorem out of this observation.


Theorem 34
Let a function f be defined by a Laurent series ∑ c_n(z − z₀)ⁿ, (with n = −∞, . . ., ∞), around a point z₀ ∈ ℂ. Assume that the series converges in a “punctured disc” {0 < |z − z₀| < R}. If infinitely many of the terms c_n, for n < 0, are not zero, then z₀ is an essential singularity of f.

Proof
Obviously z₀ is not a removable singularity. If it were a pole of order n, then all the terms c_m, for m < −n must vanish. The only remaining possibility is that z₀ is an essential singularity.

• Complex Analysis: #14 Isolated Singularities

A “singularity” is really nothing more than a point of the complex plane where a given function is not defined. That is, if f is defined in a region G ⊂ ℂ, then any point a ∉ G can be thought of as being a singularity of the function. But this is not really what we are thinking about when we speak of singularities. As an example of what we are thinking about, consider the particular function

Here, except for the special point z₀ = 0 which is not so nice, we have a good example of an analytic function. Since only a single point is causing problems with this function, let us more or less ignore this point and call it an isolated singularity. So in general, an isolated singularity is a point z₀ ∈ ℂ such that z₀ ∉ G, yet there exists some r > 0 with B(z₀, r) \ {z₀} ⊂ G.

Definition 11
Let f : G → ℂ be analytic, but with an isolated singularity at z₀ ∈ ℂ. The residue of f at z₀ is the number

According to Cauchy’s theorem, the residue is a well-defined number, independent of the radius r of the circle of the path used to define it, as long as r is small enough to satisfy our condition.

We identify three different kinds of isolated singularities:

• removable singularities, 
• poles,
• essential singularities. 

Let’s begin with removable singularities. Let f : G → ℂ have a singularity at z₀. This singularity is removable if it is possible to find some number w₀ such that if we simply define f₀ : G ∪ {z₀} → ℂ by

then f₀ is analytic (thus also differentiable at the special point z₀). We see then that a removable singularity is really nothing special. We have simply “forgotten” to put in the correct value of the function f at the isolated point z₀. By putting in the correct value, the singularity disappears.

A pole is somewhat more interesting. For example the function

has a “simple” pole at the point z₀ = 0. But then if we multiply f with the “simple” polynomial g(z) = z, then we get f(z) · g(z) = 1. Of course the function f · g has a removable singularity at the special point z₀ = 0. Furthermore, the function which results does not have a zero at the point 0. The general rule is: let z₀ be an isolated, not removable, singularity of the analytic function f. If there is some n ∈ ℕ such that the function given by f(z) · (z − z₀)ⁿ has a removable singularity at z₀, and the resulting function does not have a zero at z₀, then z₀ is a pole of order n.

Finally, an essential singularity is neither removable, nor is it a pole.

Definition 12
Let f : G → ℂ be analytic, such that all it’s isolated singularities are either removable or else they are poles. Then f is called a meromorphic function (defined in G).

• Complex Analysis: #13 Weierstrass`s Convergence Theorem

This is the analog of the theorem in real analysis which states that a sequence of continuous functions which is uniformly convergent converges to a continuous function. But here we are concerned with analytic functions.


Theorem 28 (Weierstrass)
Let G₁ ⊂ G₂ ⊂ · · · ⊂ G_n ⊂ · · · be an increasing sequence of regions in ℂ and let (f_n)_n∈ℕ be a sequence of analytic functions f_n : G_n → ℂ for each n. Let G = ∪_n=1^∞ G_n (that is, n = 1, . . ., ∞), and assume that in every compact subset of G, the sequence (f_n) converges uniformly. Let f : G → ℂ be defined by f(z) = lim_n→∞ f_n(z) for all z ∈ G. Then f is analytic on G, and furthermore f_n' → f ' uniformly on every compact subset of G.

Proof
Let z₀ ∈ G and take r > 0 such that B(z₀, r) ⊂ G. (That is the closure of the open set B(z₀, r).) Let N ∈ ℕ be sufficiently large that B(z₀, r) ⊂ ∪_n=1^N G_n. Then B(z₀, r) ⊂ G_m, for all m ≥ N. According to theorem 2 we have ∫_γf_n(z)dz = 0 for all triangles in B(z₀, r). Moreover we have

owing to the uniform convergence of the sequence. Therefore, by theorem 10, f is analytic. By Goursat’s theorem, the derivatives are also analytic. Specifically, let ζ be the boundary of the disc B(z₀, r). Then, using Cauchy’s formula (theorem 6), we have

and the fact that the convergence of the f_n is uniform in B(z₀, r) shows that f_n' → f ' uniformly.

An interesting example of this is Riemann’s Zeta function. Let z = x + iy with x > 1. Then

Thus the infinte sum ζ(z) = ∑ n^−z  (with n =1, . . . , ∞) defines a function which is the limit of a uniformly convergent sequence of analytic functions (the partial sums) for all z with Re(z) > a, where a > 1 is a given constant. Therefore Weierstrass’s convergence theorem implies that the Zeta function ζ(z) is analytic in this region. As a matter of fact, Riemann showed that, with the exception of the obvious isolated singularity at the point z = 1, the zeta function can be analytically continued throughout the whole complex plane. The big question is “Where are the zeros of the zeta function?” Some of them are located at negative even integers. (These are the so-called “trivial zeros”.) They are not particularly interesting. But there are lots along the vertical line Re(z) = 1/2. The famous Riemann conjecture — which is certainly the greatest unsolved problem in mathematics today — is that all of the zeros (apart from the trivial ones) lie on this line. [An American businessman, Mr. Landon T. Clay has put aside one million American dollars each for the solution of a certain collection of outstanding problems in mathematics. The Riemann conjecture is one of them.]

Complex Analysis: #12 Index of Point with Respect to a Closed Path

• Complex Analysis: #12 Index of a Point with Respect to a Closed Path

Let γ : [t₀, t₁] → ℂ be a continuous closed curve. Let z₀ ∈ ℂ be a point not on the path. Then, as we have seen in Exercise 2.2, we can define a continuous path θ : [t₀, t₁] → ℝ with θ(t₀) = 0 and

for all t ∈ [t₀, t₁]


Definition 10
The number θ(t₁) ∈ ℤ is called the index of the point z₀ with respect to the closed path γ. Sometimes it is also called the winding number of γ with respect to z₀. It is denoted ν_γ(z₀).


Theorem 24
Let α and β be homotopic closed paths, homotopic by a homotopy H : Q → ℂ. Assume that z₀ ∉ H(Q). then ν_α(z₀) = ν_β(z₀).

Proof
Let θ_α be the corresponding path in ℝ (corresponding to α) and let θ_β be the path in ℝ corresponding to β. Then the homotopy from α to β induces a homotopy of the path θ_α to θ_β in ℝ. Since the endpoints thus remain fixed, the index remains unchanged.


Theorem 25
Let γ, z₀ and ν_γ(z₀) be as in the definition (but this time we assume that γ is continuously differentiable). Then

Proof
Obviously the function 1/(z − z₀) is analytic in ℂ \ {z₀}. For simplicity, assume that z₀ = 0 and γ(0) = γ(1) = 1 = e^i·0 , where γ : [0, 1] → ℂ \ {0}. Write γ(t) = r(t)e^2πiθ(t). Let

h_τ(t) = e^2πiθ(t)(t + (1 − t)r(t)),

for τ, t ∈ [0, 1]. This defines a homotopy from γ to a new path γ, which lies on the unit circle. But

Theorem 26 (Cauchy’s Theorem: Complicated version)
Let f : G → ℂ be an analytic function defined in a region G of ℂ. Let γ : [0, 1] → G be a continuous closed path in G such that ν_γ(a) = 0 for all a ∉ G. Then ∫_αf(z)dz = 0.

Proof
Since the (image of the) path γ is a compact subset of G, there exists an ∈ > 0 such that for all t ∈ [0, 1], we have B(γ(t), ∈ ) ⊂ G. Let n ∈ ℕ be sufficiently large that 1/n < ∈ /√2. Then split up the whole complex plane ℂ into a system of small squares of the form

where p, q ∈ ℤ. γ meets only finitely many of these small squares, and each of the squares which γ does meet is completely contained in G. Our proof now consists in altering γ, one step after the next, through processes which can be achieved using a homotopy. In the end we get a version of γ which is so simple that the theorem becomes obvious.

• Let Q be one of the squares which γ meets. If γ only runs along the boundary of Q without entering it’s interior, then there is nothing further to do in this step of the proof. On the other hand, if γ does enter the interior of Q, then we perform a homotopy on it, moving it to the boundary of Q, but leaving all points of γ which are not in the interior of Q unchanged. Basically, we take an interior point of Q which is not a point of the path, then we push the part of γ which is in the interior of Q radially from that point out to the boundary. Do this with all the Q’s which are on the path, then finally, if necessary, move the endpoint γ(0) = γ(1) to a vertex of one of these squares. [Alternatively, and without loss of generality, we may assume that the endpoint of γ is already in a corner of the lattice] The end result of all this is a homotopy, moving γ so that at the end of the movement it is contained within the lattice of vertical and horizontal lines which make up the boundaries of all the small squares. For simplicity, let us again call this “simplified” version of the path γ.



• Now it may be that this simplified γ is still too complicated. Looking at each individual segment of the lattice, it may be that during a traverse of some particular segment, we see that γ moves back and forth in some irregular way. So again using a homotopy, we can replace γ with a new version which traverses each segment of the lattice in a simple linear path.



• We are still not completely happy with the version of γ which has been obtained, for it might be that γ has a winding number which is not zero with respect to one of the squares Q. That is, let q be an interior point of Q. What is ν_γ(q)? If it is not zero, then we can alter γ using a homotopy, changing the winding number with respect to this particular square to zero and not altering the winding number with respect to any of the other squares. The idea is simply to add a bit on to the end of γ, going out to a corner of the offending square along the lattice, then around the square a sufficient number of times to reduce the winding number to zero, returning to that corner, then returning back along the same path through the lattice to the starting point. Since γ is compact, there can be at most finitely many such offending squares. At the end of this operation, we have ensured that γ has winding number zero with respect to all points of ℂ which do not lie on the path γ.

Our curve is now sufficiently well simplified for our purposes. The reason for this is that for every segment of the lattice which γ traverses, it must be that it traverses the segment the same number of times in the one direction as it does in the other direction. To see this, let S be some segment of the lattice. To visualize the situation, imagine that it is a vertical segment. Assume that γ traverses the segment u times in the upwards direction, and d times in the downwards direction. Now S adjoins two squares, say Q₁ on the left-hand side, and Q₂ on the right-hand side. Let us now alter γ, moving the downwards moving parts which traverse S leftwards across Q₁ to the other three sides of Q₁. On the other hand, the upwards moving parts of γ are moved rightwards across Q₂ to the other three sides of Q₂. Let z₁ be the middle point of the square Q₁, and let z₂ be the middle point of Q₂. Before this movement, the winding number of γ with respect to both points was zero. However, afterwards, ν_γ(z₁) = a and ν_γ(z₂) = b. Yet they are in the same region of ℂ\ γ. Thus the points must have the same winding numbers and so a = b.

Finally, after all this fiddling, we see that we must have ∫_γf(z)dz = 0 since the total of the contributions from the path integrals along each of the segments of the lattice adds up to zero in γ each case.

Up to now we have always been performing path integrals around single closed paths. This is quite sensible. But sometimes it is also convenient to imagine two or more closed paths. So let say γ₁, . . . , γ_n be n paths, each of which are piecewise continuously differentiable and closed in some region G. We can think of them together, and call them a cycle, denoted by the letter Ω say. [More generally, we might allow paths which are not necessarily closed. In this case one speaks of “chains”, but we will not persue this idea further in this here.] Then if f : G → ℂ is a function, we might be able to perform the path integrals over each of the γ_j separately, and thus we can define the integral over the whole cycle to be simply the sum of the separate integrals.

Furthermore, if Ω is a cycle and z₀ is a point not on any path of the cycle, then we can define the index of z₀ with respect to the cycle to be the sum of the indices of z₀ with respect to the individual closed paths in the cycle. On the other hand, if we want, we can connect the endpoints of the paths in a cycle together to make a single larger closed path, thus showing that theorem 26 is also true for cycles.


Theorem 27
Again, let G ⊂ ℂ be a region, f : G → ℂ be analytic, γ a closed curve in G with winding number zero with respect to all points of ℂ not in G. Let z₀ ∈ G be a point which does not lie on the path γ, then

Proof
This is a straight-forward generalization of theorem 6. For r > 0 sufficiently small, we have

Let β(t) = z₀ + r · e^2πit be the path we are thinking about in this path-integral. (Here t ∈ [0, 1].) Obviously we have ν_β(z₀) = 1. Now take the cycle consisting of the given path γ, together with −ν_γ(z₀) copies of the path β. (If this is a negative number, then we should travel around β in the reverse direction.) We assume that r is so small that the closed disc D(z₀, r) is contained in G and furthermore the path γ does not meet D(z₀, r). Then z₀ has index zero with respect to the cycle consisting of γ − ν_γ(z₀)β. Thus, according to theorem 26,