Complex Analysis: #3 Path Integrals
Let γ(t) = γr(t) + iγi(t), where γr, γi: [t0, t1] → ℜ are real-valued functions. Then we say that the path is continuously differentiable if both the functions γr and γi are continuously differentiable. In this case, γ' = γr' + iγi' is also a path in ℂ. [Thinking in terms of 2-dimensional real geometry, we can say that γ'(t) is the "tangent vector" to γ(t).] We also learned that continuously differential paths are always rectifiable, and we have
All of this has already been dealt with in the analysis lecture. For us now, the interesting thing is to think about path integrals through a region where a complex-valued function is given.
Definition 3
Let G ⊂ ℂ be a region, and let f : G → ℂ be a function. Furthermore, let γ : [t0, t1] → G be a differentiable path. Then the path integral of f along γ is
assuming it exists.
The integral here is simply the sum of the integrals over the real and the imaginary parts. It is not necessary to assume that γ is continuously differentiable, but we will assume that it is piecewise continuously differentiable. That is, there is a partition of the interval [t0, t1] such that it is continuously differentiable along the pieces of the partition. So from now on, we will (almost) always assume that all paths considered are piecewise continuously differentiable.
As an exercise (using the substitution rule for integrals), one sees that the path integral does not depend on the way the path is parameterized. The simplest case is that, say γ(t) = t. Then (taking t from 0 to 1) we just have ∫γ f(z)dz = ∫01 f(t)dt. Almost equally simple is the case that γ(t) = it. Then we have ∫γ f(z)dz = i∫01 f(it)dt.
Increasing the complexity of our thoughts ever so slightly, we arrive at the first version of Cauchy’s integral theorem.


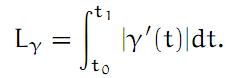

No comments:
Post a Comment
If it's a past exam question, do not include links to the paper. Only the reference.
Comments will only be published after moderation