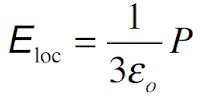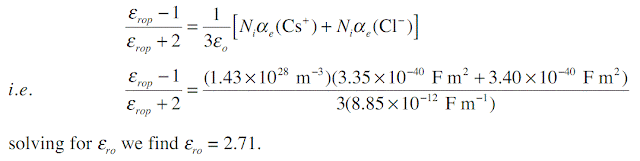• Clausius Mossotti Equation | Static relative Permittivity | Polarization of Dielectric Materials

Total Polarization 
In the presence of electronic, ionic and dipolar polarization mechanisms, the average induced dipole moment per molecule p_av will be the sum of all the contributions in terms of the local field (effective field) acting on each individual molecule,

where α_e, α_i and α_d are the electronic, ionic and dipolar (orientational) polarizabilities. E_loc is the local field, the effective field, at the site of an individual molecule that causes the induced polarization. Each effect adds linearly to the net dipole moment per molecule which is a fact verified by experiments. Interfacial polarization cannot be simply added to the above as α_if E_loc because it occurs at interfaces and cannot be put into an average polarization per molecule in the bulk.

Further, the fields are not well defined at the interfaces. In the simplest case (valid for gases), we can take the local field to be the same field (average field in the sample). This means that E_loc = E and therefore polarization Since P = Np_av, where N is the number of atoms or molecules per unit volume,

where α is the polarizability of the molecule. In solids we have to consider the actual effective field acting on a molecule. In the case of electronic and ionic polarization, the local field for cubic crystals and isotropic materials (such as liquids) can be shown to be given by the Lorentz field

The dielectric constant ε_r under electronic and ionic polarizations is then given by the Clausius Mossotti equation,

where ε_r is the relative permittivity at low frequencies, α_e is the electronic polarization, N_i is the number of ions (or atoms) per unit volume exhibiting electronic polarization, α_i is the effective ionic polarizability per ion pair and N_i is the number of ion pairs per unit volume.

Above the frequencies for ionic polarization relaxation, only electronic polarization will contribute to the relative permittivity, which will be lowered to ε_rop (relative permittivity at optical frequencies) and given by

In the case of dipolar materials (orientational polarization), we cannot use the simple Lorentz local field approximation. That is, the Clausius-Mossotti equation does not work with dipolar dielectrics and the calculation of the local field is quite complicated.

Table 1 summarizes the various polarization mechanisms and the corresponding static (or very low frequency) dielectric constant, and gives typical examples where one mechanism dominates over others.

Table 1
Typical examples of polarization mechanisms.

1. Problem: Electronic polarizability of non-polar gases

 The electronic polarizability of the Ar atom is 1.7 × 10^-40 F m². What is the static dielectric constant of Ar gas at 1 atmosphere at room temperature (300 K)?  


Solution
To calculate ε_r we need the number of Ar atoms per unit volume, N. If P is the pressure, V is the volume and N′ is the total number of atoms, then the ideal gas law is

PV = (N′/N_A)RT 

where R is the gas constant and T is the absolute temperature and N′/N is the number of moles of gas. Then, P = NkT where N = N ′/V, is the number of atoms per unit volume and k = R / N_A, is the Boltzmann constant. Thus,

Using the Clausius-Mossotti equation, Equation (2), gives the same result because when Nα_e is small as in the case of gases, the Clausius-Mossotti equation simplifies to Equation (1). The reader can verify this by expanding Equation (2) in a series in terms of (Nα_e) and neglecting terms greater than the linear term. The dielectric constant of most gases is small for one major reason. The number of atoms or molecules per unit volume N is very small compared with the number of atoms or molecules in the liquid and solid states. Generally the dielectric constant of most nonpolar gases (including air) can be takes as 1, the same as vacuum except at very high pressures.




2. Problem: Electronic polarizability of a van der Waals solid

The electronic polarizability of the Ar atom is 1.7 × 10^-40 F m². What is the static dielectric constant of solid Ar (an FCC crystal below 84 K) if its density is 1.8 g cm^-3?


Solution
 To calculate ε_r we need the number of Ar atoms per unit volume N from the density d. If  M_at = 39.95 g mol^-1 is the relative atomic mass of Ar and N_A is Avogadro's number then we have,

The two values are different by about 17%. The simple relationship in Equation (1) underestimates the relative permittivity and would be appropriate for gaseous Ar.




3. Problem: Relative permittivity of ionic crystals

Consider a CsCl crystal which has the CsCl unit cell crystal structure (one Cs⁺–Cl^- pair per unit cell) with a lattice parameter (a) of 0.412 nm. The electronic polarizability of Cs⁺ and Cl^- ions are 3.35 × 10 ^-40 F m², and 3.40 × 10^-40 F m² respectively, and the mean ionic polarizability per ion pair is 6 × 10^-40 . What is the low frequency dielectric constant and that at optical frequencies?

Solution
The CsCl structure has one action (Cs⁺) and one anion (Cl^-) in the unit cell. Given the lattice parameter a = 0.412 × 10^-9m, number of ion pairs N_i per unit volume is

At high frequencies, that is near optical frequencies, the ionic polarization is too sluggish to allow ionic polarization to contribute to ε_r. Thus, ε_rop, relative permittivity at optical frequencies, is given by

Note that experimental values are ε_r = 7.20 at low frequencies and ε_rop = 2.62, very close to calculated values.




4. Problem: Dielectric constant of water (a dipolar liquid)

Given the static dielectric constant of water as 80, its density as 1 g cm^-3, calculate the permanent dipole moment p₀ per water molecule assuming that it is the orientational polarization of individual molecules that gives rise to the dielectric constant. Use both the simple relationship in Equation (1) and also the Clausius-Mossotti equation and compare your results with the permanent dipole moment of the water molecule which is 6.1 × 10^-30C m.  


Solution
We first need the number of H₂O molecules per unit volume. The molecular mass, M_mol is 18 × 10^-3 kg mol^-1, its density d is 10³kg m^-3. The number of H₂O molecules per unit volume N_d is

This is three times greater than the actual permanent dipole moment of H₂O (∼ 6 × 10^-30 C m). On the other hand, if we use the Clausius-Mossotti equation we find p₀ = 3.1 × 10^-30 C m, which is half the actual permanent dipole moment of H₂O. Both are unsatisfactory calculations. The reasons for the differences are two fold. First is that the individual H₂O molecules are not totally free to rotate. In the liquid, H₂O molecules cluster together through hydrogen bonding so that the rotation of individual molecules is then limited by this bonding. Secondly, the local field can neither be totally neglected nor taken as the Lorentz field. A better theory for dipolar liquids is based on the Onsager theory which is beyond the scope of this document. Interestingly, if we use the actual p₀ = 6.1 × 10^-30 C m in the Clausius-Mossotti equation, then ε_r turns out to be negative, which is nonsense.





USEFUL DEFINITIONS  

Avogadro's number (N_A) is the number of atoms in exactly 12 grams of Carbon-12. It is 6.022 × 10²³. Since atomic mass is defined as 1/12 of the mass of the carbon-12 atom, N_A number of atoms of any substance has a mass equal to the atomic mass, M_at, in grams.  

Boltzmann’s constant k is the gas constant per atom or per molecule, that is, the gas constant divided by Avogadro’s number (k = R/N_A); k = 1.38 × 10^-23 J K^-1. (3/2kT is the mean kinetic energy associated with the translational motions of gas molecules in a gas cylinder at temperature T).

Clausius-Mossotti equation relates the dielectric constant (ε_r), a macroscopic property, to the  polarizability (α), a microscopic property.  

Dielectric is a material in which energy can be stored by the polarization of the molecules. It is a material that increases the capacitance or charge storage ability of a capacitor. Ideally it is a non-conductor of electrical charge so that an applied field does not cause a flow of charge but instead a relative displacement of opposite bound charges and hence polarization of the medium.

Dipolar (orientational) polarization arises when randomly oriented polar molecules in a dielectric are rotated and aligned by the application of a field so as to give rise to a net average dipole moment per molecule. In the absence of the field the dipoles (polar molecules) are randomly oriented and there is no average dipole moment per molecule. In the presence of the field the dipoles are rotated, some partially and some fully, to align with the field and hence give rise to a net dipole moment per molecule.  

Electronic polarization is the displacement of the electron cloud of an atom with respect to the positive nucleus. Its contribution to the relative permittivity of a solid is usually small.  

Ionic polarization is the relative displacement of oppositely charged ions in an ionic crystal that results in the polarization of the whole material. Typically ionic polarization is important in ionic crystals below the infrared wavelengths.  

Polarization is the separation of positive and negative charges in a system so that there is a net electric dipole moment per unit volume.  

Relative permittivity (ε_r) or the dielectric constant of a dielectric is the fractional increase in the stored charge per unit voltage on the capacitor plates due to the presence of the dielectric between the plates (the whole space between the plates is assumed to be filled). Alternatively we can define it as the fractional increase in the capacitance of a capacitor when the insulation between the plates is changed from vacuum to a dielectric material keeping the geometry the same.  

Valence electrons are those electrons in the outer shell of an atom. As they are the farthest away from the nucleus, they are the first electrons involved in atom-to-atom interactions.





Important Note: This article was originally written by Safa Kasap. He reserves all rights. Use this article only for educational purpose. The document can be obtained at the author`s website.

• Expression for Conductivity of ionized gas (plasma) at low pressure

A plasma is an ionized gas. As a rule, plasmas contain free electrons and positive ions. Since the ions are more massive than the electrons, the current is carried almost exclusively by the electrons.

At low pressure, we can ignore the collisions between the electrons and the gas molecules, and hence energy losses.

Considering a plane electromagnetic wave (EM wave) propagating, the motion of the charge depends almost entirely on the electric field (E-field).

The conductivity of the gas is given by where Jt is the electron current density.

Actually, Jt is the sum if all ions in the gas.

where Ni is the number of electrons or ions per metre cube, Qi is the charge of electrons or ions and dxi/dt (= vi) is the speed of the electron or ion along the x-axis.

Now, we require the velocity v of a free electron or ion of mass m subjected to an alternating electric field.

Note that the time derivative of velocity v here can be written as dv/dt = jwv ; assuming for example that v = v0 exp(jwt) where j represents the imaginary component, w the frequency and t the time.

Taking the expressions for the force, we obtain

v leads the field by 90⁰

Then, replacing this expression of v in Jt , taking the pure imaginary part (the "-90⁰") and equating the 2 equations for Jt, we get

As the mass of the ions is much larger than that of the electrons while the charge is of the same order of magnitude as that of the electrons, the contribution of the ions can be neglected.

Thus, the conductivity can be written in terms of the charge and mass of electrons only.

So, this is the simple expression that can be used to calculate the conductivity of the plasma.

• Plane Harmonic Wave Equations in Harmonic Isotropic Linear Stationary (HILS) medium

We`ll now derive the Plane Harmonic Wave Equations in Harmonic Isotropic Linear Stationary (HILS) medium from the Maxwell`s equations.

The general Maxwell`s equations are

For linearity and isotropy, we have

We will use the following identity to obtain the wave equations

To derive the wave equation for E

replacing Jfree in the equation (7)

So, we get the wave equation for E

To obtain the wave equation for B in Harmonic Isotropic Linear Stationary (HILS) medium, we follow the same principle.

Taking the divergence of B =0 (Maxwell second equation above) and writing B in terms of H as appropriate for linearity and isotropy, we obtain

From equation (4) of the Maxwell`s equations, we obtain equation (12) below, and upon simplifying and applying curl on both sides, we obtain the following form of the equation

Then, we replace the right-hand side of equation (11) and the curl of E (from the 3rd Maxwell`s equation) in equation (12)

Hence, we have obtain the wave equation for H in a HILS medium.

So, we have finally obtained the wave equations for both E and H. That`s what we wanted.



Now, let`s try an additional simplification for the wave equation for E.

let E be in the x-direction,

We can therefore replace the right-hand side of equation (9) with the result of the above equation

Equation (15) is the solution for Ex that would be obtained from (14).

As E and H are transverse, an example of a solution would be

where Z is the characteristic impedance.

Magnetic field (B-field) tangential to surface of Superconductor

• Magnetic field (B-field) is always tangential to the surface of a Superconductor

We are going to prove that magnetic fields (B-fields) are always tangential to the surface of a superconductor.

First, let`s briefly discuss what superconductivity is. Superconductivity is the sudden disappearance of all electrical resistance when the material is cooled below a certain temperature, called the critical temperature. Apart from the disappearance of all electrical resistance, what makes superconductors to be of great interest is that superconductors have extraordinary magnetic properties.

There are 2 types of superconductivity:

• Superconductivity of type I (discovered by Omnes),
• Superconductivity of type II (discovered by Bednorz and Muller)

Let`s now look at the properties of superconductors of type I.

Properties of superconductive material of type I

• There is an absence of the magnetic field (B-field) inside the superconductor. In fact, the B-field is expelled from inside of the material (B = 0 inside - Meissner-Ochsenfeld effect). This is independent of how the transition to the superconductor state occurs. (There is a loss of history) Note that in superconducting alloys, the Meissner-Ochsenfeld effect is not sharp and the field can penetrate the superconductor.
• There is a persistent current inside the material even in the absence of an electromotive force (battery).
• There is no magnetization of the material.
• Current flows along a skin (thickness ~ 10^-7m) around the boundary of the material.

Let`s now explain how the B-field is always tangential to the surface of a superconductor.

From Maxwell`s equations, we know that the divergence of B is zero (div(B) = 0). It follows that the magnetic field lines are continuous and closed. Therefore, the components of B normal to the surface, Bn must be equal on both sides of the surface, that is, both inside and outside the material.

However, from the first property mentioned above, the B-field is zero inside (so, it is also zero outside the material). It follows that the normal component at the external field at the surface outside the superconductor is also zero. This means that the magnetic field lines are tangential to the surface of the superconductor. The magnetic field lines surround the superconductor.



Additionally, as B = 0 inside, this means that the mean density of current = 0. Therefore, there is no magnetization field and no H-field.

• Magnetization in fluid in Quantum Mechanical Case

Previously, we found the equation for magnetization of a fluid in the classical case. Now, let`s find the equation for magnetization of a fluid for the quantum mechanical case.

Here, we consider the fluid to have N spins up (Nup) and N spins down (Ndown). In the presence of an external field B, the energy is given by where the positive z-axis points upwards.

Again, as in the classical case for magnetization of a fluid (Langevin`s equation), the relative probability of having any angle is, from statistical mechanics, exp(-energy/kT).

So,  and . If  N is the total number of dipoles, them M is the product of N with the average magnetic moment along the z-axis.

In most normal cases, say, for typical moments, room temperatures, and the fields one can normally get (like 10 000gauss), the ratio represented by u is about 0.02. One must go to very low temperatures to see the saturation. For normal temperatures, tanh(u) can be replaced by u and

The graph of M against u for the quantum mechanical case of magnetization in fluids resembles that for the classical case.

When B gets very large, the hyperbolic tangent approaches 1, and M approaches the limiting value (N x the average magnetic moment along the z-axis). So, at high fields, the magnetization saturates. We can see why that is,; at high enough fields, the moments are all lined up in the same direction . In other words, they are all in the spin-down state, and each atom contains the same moment.


Additionally, when we look at the expressions for magnetization in the fluid at room temperature for both the classical and quantum case, we notice that M is proportional to B/T. From this, we can derive Curie`s law which is M = kB/T, where k is a constant.

• Langevin`s Equations for Magnetization in Classical Fluid

Consider a fluid at a temperature T, with dipole moments. As the molecules collide with each other, the magnetic field exerts a mean restoring force. That is, there is a resultant magnetic moment M.

In the absence of a field, the number of randomly oriented molecules satisfy the equation

 

where N is the total number of dipoles &  is the solid angle (the whole of space).

Consider a sphere, = 4, then the solid angle at is

 

This can also be shown by the fractional surface area of a surrounding sphere. That is, the area obtained on the surface of the sphere when we are situated at an angle and we moved by an angle d, over the total surface area  of the sphere.

where dN lies between and +d

One assumes that each of the atom has a magnetic moment , which always has the same magnitude but can point in any direction.

The orientation of atomic magnetic dipoles with respect to external magnetic field B give rise to a magnetic potential energy given by , where is the angle between the moment and the field. From statistical mechanics, the relative probability of having any angle is exp(-energy/kT), so angles near zero are more likely than angles near .

Therefore dN is proportional to

where C is the Normalization constant.

Each moment contributes an amount to the magnetization parallel to the field. This is because the components will give zero value because of the symmetry of the problem.  The magnetization resulting from all dipoles within is given by

let so

Performing the integration and re-arranging gives

 

 

At normal temperature, cosh(u) can be expanded as

So, at normal temperature,

So, magnetic effects will be noticeable small at lower temperature for the case of classical fluid.

A typical graph of M against u would be as follows: