• Physics 9702 Doubts | Help Page 162

Question 806: [Dynamics > Conservation of Linear momentum]

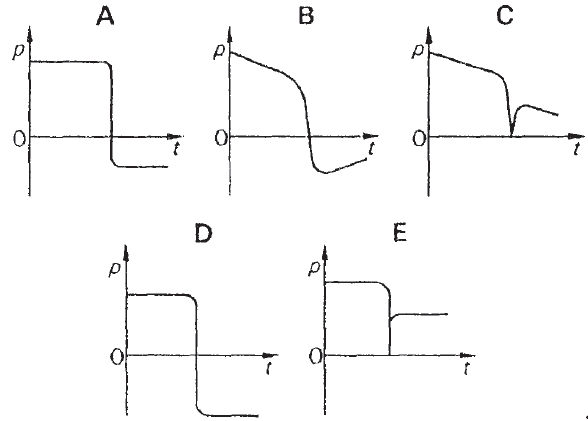
An ice-hockey puck slides along horizontal, frictionless ice-rink surface. It collides inelastically with wall at right angles to its path, and then rebounds along its original path.

Which graph shows variation with time t of the momentum p of the puck?

For J92 / I / 4:

For November 2011 Paper 11 Q12 & Paper 13 Q10:

Reference: Past Exam Paper – J92 / I / 4 & November 2011 Paper 11 Q12 & Paper 13 Q10

Solution 806:

Answer: A.

A frictionless ice-rink surface means that the speed of the puck is not affected (by friction) during its motion. Thus, it can be assumed that it moves with constant speed before collision.

Momentum p = mv

Since the speed is constant before the collision, the momentum should also be constant. [B and C are incorrect]

After the collision, the puck rebounds along its original path.

Momentum is a vector, so if the original direction of the momentum is taken as positive, the momentum after collision is negative. [D is incorrect]

The collision is inelastic, so the puck loses some of its energy. The puck moves with a lower speed after the collision, and thus has a smaller momentum. Note that the wall gains some momentum so that the total momentum is conserved in the system.

Question 807: [Current of Electricity > e.m.f.]

When a battery is connected to a resistor, battery gradually becomes warm. This causes the internal resistance of the battery to increase whilst its e.m.f. stays unchanged.

As internal resistance of the battery increases, how do the terminal potential difference and the output power change, if at all?

terminal potential difference               output power

A         decrease                                              decrease

B         decrease                                              unchanged

C         unchanged                                           decrease

D         unchanged                                           unchanged

Reference: Past Exam Paper – June 2013 Paper 11 Q33

Solution 807:

Answer: A.

Let the e.m.f. of the battery be E.

Due to its internal resistance (r), there will be some lost volts (V_L) in the battery.

V_L = Ir where I is the current provided by the battery

Let the terminal potential difference across the battery be V.

V = E – V_L

As the internal resistance (r) of the battery increases V_L also increases causes the terminal p.d. V to decrease.

Output power P of battery = VI

Since the terminal p.d. V across the battery decreases, the output power also decreases.

Note that the output power is NOT P = EI because some volts are lost inside the battery and not provided to the external circuit.

Question 808: [Measurement > Uncertainty]

Young modulus of the material of a wire is to be found. Young modulus E is given by the equation below.

E = 4Fl / πd²x

The wire is extended by a known force and the following measurements are made.

Which measurement has the largest effect on uncertainty in the value of the calculated Young modulus?

Reference: Past Exam Paper – June 2014 Paper 11 Q5

Solution 808:

Answer: B.

The percentage uncertainty in the diameter needs to be doubled since it is squared in the equation.

E = 4Fl / πd²x

ΔE / E = ΔF/F + Δl/l + 2(Δd/d) + Δx/x

ΔF / F = 0.01 / 19.62 = 0.000 51

Δl / l = 0.002 / 2.043 = 0.000 98

2 (Δd / d) = 2 (0.02 / 0.54) = 0.074 07

Δx / x = 0.2 / 5.2 = 0.038 46

So the diameter has the largest effect on the uncertainty in the value of the calculated Young modulus.

Question 809: [Waves > Intensity]

A plane wave of amplitude A is incident on surface of area S placed so that it is perpendicular to the direction of travel of the wave. The energy per unit time reaching the surface is E.

Amplitude of the wave is increased to 2 A and the area of the surface is reduced to ½ S.

How much energy per unit time reaches this smaller surface?

A 4E                            B 2E                            C E                              D ½ E

Reference: Past Exam Paper – June 2004 Paper 1 Q26

Solution 809:

Answer: B.

Intensity = Power / Surface Area

‘Energy per unit time’ is the power. So, the power is E.

Let the initial intensity be I.

I = E / S giving E = IS

The intensity is proportional to the amplitude squared. Increasing the amplitude to 2A causes the intensity to become 4I.

The area of the surface is reduced to ½ S.

New Power = New Intensity × New Area = 4I × ½ S = 2IS = 2E

Question 810: [Electric field + Kinematics]

The path of an electron with initial speed v in uniform electric field between two parallel plates is shown.

Vertical deflection x is measured at the right-hand edge of the plates.

Distance between the plates is halved. The potential difference between the plates remains the same.

What will be the new deflection of the electron with the same initial speed v?

A x                              B √2x                                    C 2x                            D 4x

Reference: Past Exam Paper – November 2014 Paper 13 Q32 & June 2017 Paper 12 Q31

Solution 810:

Answer: C.

Electric field strength, E = V / d

where V is the p.d between the plates and d is the separation

Electric force F = Eq

The distance d is halved while V remains the same.

New electric field strength = V / 0.5d = 2 (V/d) = 2E

New electric force = (2E)q = 2F

In both cases, the electron enters the field horizontally – so its initial vertical velocity is zero in both cases.

F = ma

The electric force causes a constant acceleration vertically, it does not affect the horizontal motion – so we need to only consider the vertical motion of the particle.

The deflection is measured at the end of the plates. Even if the separation of the plates have been halved, the horizontal length of the plate is still the same. In both cases, the initial speed is the same, so the time taken (t) to travel the length of the plates is the same in both cases.

Consider the vertical motions in both cases.

Equation for uniformly accelerated motion: s= ut + ½ at²  

In the 1^st case, [The force F produces an acceleration]

Deflection s = 0 + ½ at2 = ½ at²

Deflection x = ½ at²

In the 2^nd case, [The acceleration is now 2a since the force is 2F {F = ma, so 2F = m(2a) since the mass of the electron is constant}]

Deflection s = 0 + ½ (2a)t² = at² = 2(½ at²) = 2x

Question 811: [Kinematics]

A particle moves in the manner shown by velocity-time graph.

The displacement of particle has been measured so that it is zero at t = 0. Point Q refers to a point in its motion.

Reference: Past Exam Paper – June 2011 Paper 12 Q7

Solution 811:

Answer: D.

Gradient of a velocity-time graph gives the acceleration

Gradient (acceleration) is zero at the maxima and minima. [A and B are incorrect]

Displacement (NOT distance) is taken to be zero at t = 0.

In a velocity-tome graph, the displacement is given by the area under the graph. If the area is taken above the time axis, then the displacement is positive and if it is below the time axis, the displacement is negative.

As long as it is above the time axis, the displacement is positive – even if the curve is increasing or decreasing on the upper part of the time axis. So, the maximum displacement occurs when the curve touches the time axis. This is at times t = 5s and t = 15s.