Complex Analysis: #28 Stirling`s Formula
where P1(t) = t − [t] − 1/2, and [t] is the largest integer which is less than or equal to t. Of course we take the principle value of the logarithm here. The fact that, as long as z is not a negative real number, the integral on the right-hand side of the equation goes to zero as |z| → ∞, shows that
(at least if we stay away from the negative real numbers). In fact we will show that for a given fixed δ between 0 and π, we have that P1(z) falls uniformly to 0, for z = reiθ and |θ| ≤ π − δ.
Lemma 1 (Euler’s Summation formula)
Let f : ℝ → ℝ be continuously differentiable (in the sense o real analysis). Then
Taking the sum from k = 1 to n then gives the result.
Similarly we have
Lemma 2
Assume z is not a negative real number or zero. Let P2(t) = t∗(t∗ − 1)/2, where t∗ = t − [t] for t ∈ ℝ. Then we have
The function Φ which is so defined is analytic in ℂ (minus the negative reals and 0).
Proof
Using partial integration, we have
where K is a finite number. (When z is a positive real number, the integral obviously also convergesThus we can use Weierstrass’ convergence theorem — on the integrals between successive integer— to conclude that Φ is an analytic function.
Lemma 3
We have
Proof
This follows from the previous lemma, since then K = 0 and π/2y → 0, when y → ∞.
So now that we have looked at these lemmas, let us begin proving Stirling’s formula. It involves the standard, rather awkward problem of the logarithms. So to avoid this, let us first take the case that z is just a positive real number. That is, we take z = x + i · 0, and we set about examining log Γ (x). Obviously Γ (x) > 0, so we can use the simple, real logarithm function. The antiderivative of log(x) is x log(x) − x. Therefore, using lemma 1, we see that for n ∈ ℕ we have
is simply some constant real number, let’s call it C. But then we see that the left-hand side of the equation, namely log Γ (x) is just the restriction to the positive real numbers of an analytic function which is defined in the region consisting of C with the negative real numbers and 0 removed. Similarly the right-hand side, namely xlog x − (log x)/2 − x − Φ(x) + C is the restriction to the positive real numbers of another analytic function which is defined in the same region. Since both of these functions coincide on the positive real numbers, they must be same analytic function.
So the only remaining problem is to find out what the value of C is. Writing
Γ(1 − z) = −zΓ(−z),
we have
This is true for all y > 0, no matter how large. But according to lemma 3, we have limy→∞Φ(iy) = 0. For the rest, we should remember that for a complex number of the form reiθ, we have



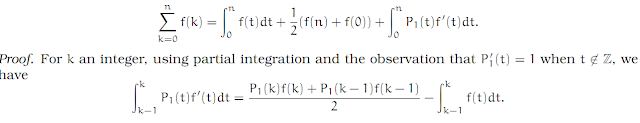




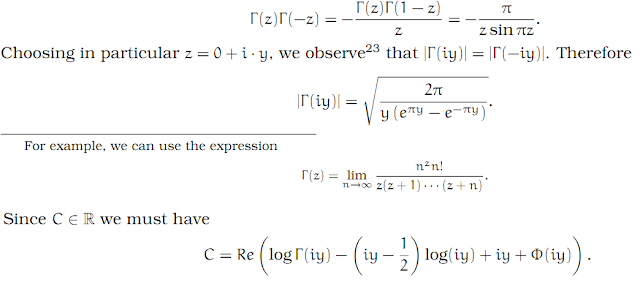

No comments:
Post a Comment
If it's a past exam question, do not include links to the paper. Only the reference.
Comments will only be published after moderation