Complex Analysis: #24 Infinite Products of Functions
converging. In fact it is absolutely convergent. Therefore, according to theorem 47, we must have
converging, and so defining a function, for all z ∉ ℤ. But is this function meromorphic? It is a small exercise to see that the sequence of partial products is uniformly convergent on compact subsets of ℂ \ ℤ, and thus according to Weierstrass’ convergence theorem, the function is analytic in ℂ \ ℤ. So this example shows one way to proceed in this special case.
On the other hand, polynomials seem to give us a more natural basis for generating analytic functions. Given a polynomial P(z), we can write it as
P(z) = a(a1
− z) · · · (an
− z),
where a1, . . . , an are the zeros of the polynomial (perhaps some with multiplicity greater than one), and a ≠ 0 is some constant. If we generalize this to an infinite product, and if we hope that things will converge, then we expect the terms to converge to 1. So it is natural to write something like this:
If the sequence of absolute values |an| grows sufficiently rapidly, then we might expect to have convergence. But even a simple sequence like an = n does not satisfy this property. Such considerations led to Weierstrass’ product theorem.
Theorem 48 (Weierstrass)
Let (an)n∈ℕ be a sequence of complex numbers with an ≠ 0 for all n, and limn→∞ an = ∞. Then there exist integers mn ≥ 0 such that the product
In fact, we can be more specific than this.
Corollary
Let f : ℂ → ℂ be a non-constant entire function. Then there exists an entire function g such that
we have that the function given by φ(z) = f(z)/Ψ(z) is an entire function (with removable singularities) with φ(z) ≠ 0, for all z ∈ ℂ. But then φ'(z)/φ(z) is also an entire function, with antiderivative g(z), say. Let’s look at the derivative of the function φ(z)e−g(z). We get
So φ(z)e−g(z) is a constant, which we can absorb into g in such a way that φ(z)e−g(z) = 1
A simple consequence of this theorem is that every meromorphic function defined throughout ℂ is a rational function. That is, let f be meromorphic, with poles a1, a2, . . . . [ Of course if there are only finitely many poles, then this is trivial. On the other hand, since the poles are isolated, there can be at most countably many of them.] Regardless of the way the poles are numbered, since they are isolated we must have limn→∞ an = ∞. Therefore take the product Ψ · f, where Ψ is an entire function with the same set of zeros as f has poles (weighted according to their orders). Thus Ψ · f is — apart from a set of isolated, removable singularities — an entire function; call it g : ℂ → ℂ. Therefore we can write f = g/Ψ.
Looking at the the formula in Weierstrass’ theorem, we see that it can become a bit of a mess, particularly then the numbers mn get larger and larger. Things are nicer if there exists a single number m, such that Weierstrass’ theorem works with all mn ≤ m.
Definition 16
Given a countable set of non-zero complex numbers {an}, if there exists an integer m ≥ 0 such that the product
converges, then this is called the canonical product associated with the sequence (an)n∈ℕ. The smallest such m is called the genus of the canonical product.
When does the canonical product exist? That is to say, for a fixed non-negative integer m, and for each an, we have a “remainder term” of the form





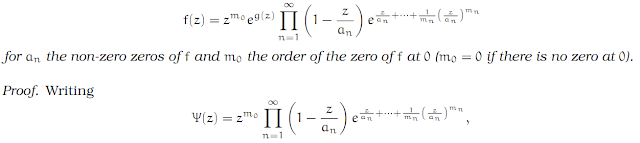



No comments:
Post a Comment
If it's a past exam question, do not include links to the paper. Only the reference.
Comments will only be published after moderation