Complex Analysis: #25 Some Infinite Products
Given a sequence of non-zero points an with ∑ 1/|an| converging, we can simply say that
gives us an example of a genus zero function with zeros just where we want them. Of course if we also want a zero at 0, then we can multiply this product with the factor Czl say, where l is the order of this zero, and C is a non-zero constant which we can choose as we like.
The sine function:
Being more concrete, let us look at the function sin πz. According to the definition of the sine function, we have
But this can only be zero if eiπz = e−iπz. Writing z = x + iy, this means that e−yeiπx = eye−iπx. In particular, y = 0 so that the zeros are just the familiar zeros which we know from real analysis, namely the integers, ℤ. As we know, the series ∑ 1/n2 converges, thus the complex sine function must have genus one. Writing
the problem is then to determine the function g. For this, we take the logarithmic derivatives of both sides. We obtain
so that the sum is uniformly convergent in compact subsets of ℂ which do not contain points of ℤ, thus showing that the derivative of the sum is the sum of the derivatives.)
Therefore
where C is a constant. On the other hand, we have both cot(w) = −cot(−w) and χ(w) = −χ(−w). That is, they are both anti-symmetric. But this can only be true if the constant C = 0. But this implies that our function g satisfies the equation g '(z) = 0; that is, g is a constant. Since






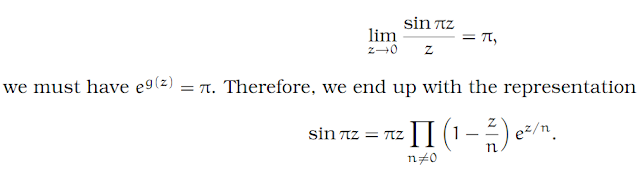
No comments:
Post a Comment
If it's a past exam question, do not include links to the paper. Only the reference.
Comments will only be published after moderation