Complex Analysis: #19 Integrating Out From a Pole
where 0 is a pole, and ∞ is a zero of f. For example, look at the function f(x) = 1/x. But here we see big problems! Both of the integrals ∫1∞ f(x)dx and ∫01 f(x)dx are divergent.
Thinking about this, we see that the problems with the function 1/x stem from the fact that, first of all, the zero at ∞ is simple, and second of all, the pole at 0 is simple. This leads us to formulate the following theorem.
Theorem 39
Again, let R be a rational function defined throughout ℂ, but this time with a zero of order at least 2 at ∞. Furthermore, R has no poles in the positive real numbers (x > 0), and at most a simple pole at 0. Then we have
for all 0 < λ < 1.
Proof
As before, the function zλR(z) has at most finitely many poles in ℂ. Let γr, φ, where 0 < r < 1 and 0 < φ < π, be the following closed curve. It starts at the point reφi and follows a straight line out to the point Teφi, where T = 1/r. Next it travels counter-clockwise around the circle of radius T, centered at 0, till it reaches the point Te(2π−φ)i. Next it travels along a straight line to the point re(2π−φ)i. Finally it travels back to the starting point, following the circle of radius r in a clockwise direction. Lets call these segments of the path L1, L2, L3 and L4. By choosing r and φ to be sufficiently small, we ensure that the path γr, φ encloses all poles of the function. In the exercises, we have seen that the path integrals along the segments L2 and L4 tend to zero for r → 0. Thus we have



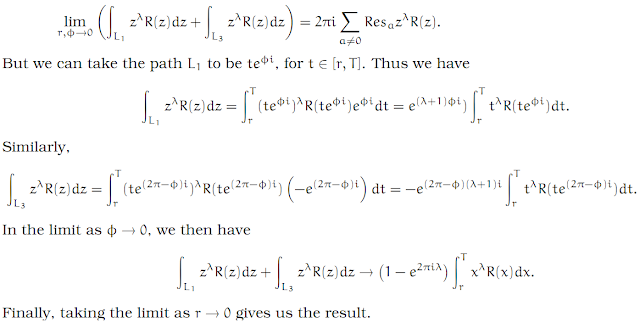
No comments:
Post a Comment
If it's a past exam question, do not include links to the paper. Only the reference.
Comments will only be published after moderation