Complex Analysis: #17 Residues Around the Point at "Infinity"
Definition 13
Let G ⊂ ℂ ∪ {∞} be a region containing ∞. (Thus G is open and connected.) [Note that we must then have ℂ \ G being a closed and bounded set, thus compact.] We will say that f : G → ℂ is analytic at ∞ if the function given by f(1/z) has a removable singularity at 0. Similarly, f has a zero of order n, or a pole of order n at ∞ if the respective property is true of the function f(1/z) at 0. That is to say, if ∞ is a zero of order n of f then we would like to have the function wnf(w) having a removable, non-zero singularity at ∞. However this is the same as looking at the limit as z → 0 of the function which is given by substituting w = 1/z. That is, the function
So f has a zero of order n at infinity if g has a removable, non-zero singularity at 0.
Theorem 36
Let g, h : ℂ → ℂ be entire, not constant, functions (thus they are analytic at all points of ℂ). Let f be the meromorphic function f = g/h. Assume that there is no zero of h on the real number line. Assume furthermore that f has a zero at infinity of order at least 2. Then we have
(Here the sum is over all poles of the function f in the “upper” half plane of ℂ. That is, the set of all complex numbers with positive imaginary parts.)
Proof
Because f has a zero at infinity, we have f being bounded outside of a compact disc of the form D = {z ∈ ℂ : |z| ≥ r}, for some sufficiently large r > 0. In particular, all of the poles of f must be within D. Since the zeros of h are isolated, there are only finitely many of them, thus the sum over the poles is finite. Therefore, the residue theorem shows that
where γ is the closed curve which consists of two segments: first the segment along the real number line from −r to r, then the segment consisting of the semi-circle of radius r around zero, traveling upwards from r and around through ir, then coming back to −r. That is to say,
We are assuming that f has a zero at infinity of order at least 2. That means, for all ∈ > 0 there exists some δ > 0 such that for all w ≠ 0 in ℂ with |w| < δ, we have
Since ∈ can be taken to be arbitrarily small, giving a corresponding δ, we can choose our r to be greater than 1/δ, and thus the integral around the half-circle αr is small. The limit r → ∞ gives the formula of the theorem.
So this gives a method of calculating an integral along the real number line without actually having to do the integral at all! We only need to know the residues of the poles of the function in the upper half-plane of ℂ; no poles are allowed to be on the real number line; and the function should tend to zero sufficiently quickly at infinity.
But the assumption that the zero at infinity is of order 2 or more might be too restrictive. Perhaps the function we happen to be looking at only has a simple zero at infinity. For example consider the function
The integral along the real number line does not converge, and so this shows that we cannot expect the integral to exist if the zero at infinity is only of the first order. But perhaps the following theorem, where f(x) is multiplied with the “rotating” function eix, thus mixing things up nicely, might be useful. However, in contrast to the case where the zero at infinity is of at least second order, here we cannot expect that the integral over the absolute value of the function also converges.
Theorem 37
The same assumptions as in the previous theorem, except that the zero of f at infinity is only of the first order. Then we have
Proof
Again, we only have finitely many singularities in the upper half-plane. This time take a closed path γ consisting of four straight segments. The first segment is the straight line from the point −r to +r, along the real number line. The second segment goes from r to r + ir. The third from r + ir to −r + ir, and the fourth from −r + ir back to the starting point at −r. Let’s call these segments γ1(r), . . . , γ4(r). Following the ideas in the proof of the previous theorem, we see that it is only necessary to show that
for j = 2, 3, 4. Our assumption implies that for all ∈ > 0 there exists an r0 > 0 such that |f(z)| < ∈ for all z with |z| > r0. We will show that the absolute value of the integral along the path γ2(r0) is less than ∈ . The calculation for the other paths is similar. We have





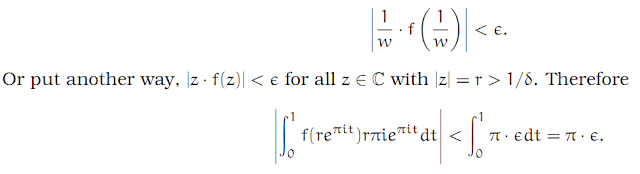



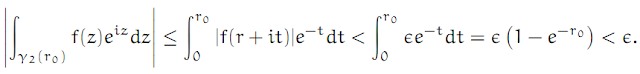
No comments:
Post a Comment
If it's a past exam question, do not include links to the paper. Only the reference.
Comments will only be published after moderation