• Langevin`s Equations for Magnetization in Classical Fluid

Consider a fluid at a temperature T, with dipole moments. As the molecules collide with each other, the magnetic field exerts a mean restoring force. That is, there is a resultant magnetic moment M.

In the absence of a field, the number of randomly oriented molecules satisfy the equation

 

where N is the total number of dipoles &  is the solid angle (the whole of space).

Consider a sphere, = 4, then the solid angle at is

 

This can also be shown by the fractional surface area of a surrounding sphere. That is, the area obtained on the surface of the sphere when we are situated at an angle 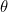and we moved by an angle d, over the total surface area  of the sphere.

where dN lies between and +d

One assumes that each of the atom has a magnetic moment , which always has the same magnitude but can point in any direction.

The orientation of atomic magnetic dipoles with respect to external magnetic field B give rise to a magnetic potential energy given by , where is the angle between the moment and the field. From statistical mechanics, the relative probability of having any angle is exp(-energy/kT), so angles near zero are more likely than angles near .

Therefore dN is proportional to

where C is the Normalization constant.

Each moment contributes an amount to the magnetization parallel to the field. This is because the components will give zero value because of the symmetry of the problem.  The magnetization resulting from all dipoles within is given by

let so

Performing the integration and re-arranging gives

 

 

At normal temperature, cosh(u) can be expanded as

So, at normal temperature,

So, magnetic effects will be noticeable small at lower temperature for the case of classical fluid.

A typical graph of M against u would be as follows: