Clausius Mossotti Equation | Static relative Permittivity | Polarization of Dielectric Materials
In the presence of electronic, ionic and dipolar polarization mechanisms, the average induced dipole moment per molecule pav will be the sum of all the contributions in terms of the local field (effective field) acting on each individual molecule,
where αe, αi and αd are the electronic, ionic and dipolar (orientational) polarizabilities. Eloc is the local field, the effective field, at the site of an individual molecule that causes the induced polarization. Each effect adds linearly to the net dipole moment per molecule which is a fact verified by experiments. Interfacial polarization cannot be simply added to the above as αif Eloc because it occurs at interfaces and cannot be put into an average polarization per molecule in the bulk.
Further, the fields are not well defined at the interfaces. In the simplest case (valid for gases), we can take the local field to be the same field (average field in the sample). This means that Eloc = E and therefore polarization
Since P = Npav, where N is the number of atoms or molecules per unit volume,
where α is the polarizability of the molecule. In solids we have to consider the actual effective field acting on a molecule. In the case of electronic and ionic polarization, the local field for cubic crystals and isotropic materials (such as liquids) can be shown to be given by the Lorentz field
where εr is the relative permittivity at low frequencies, αe is the electronic polarization, Ni is the number of ions (or atoms) per unit volume exhibiting electronic polarization, αi is the effective ionic polarizability per ion pair and Ni is the number of ion pairs per unit volume.
Above the frequencies for ionic polarization relaxation, only electronic polarization will contribute to the relative permittivity, which will be lowered to εrop (relative permittivity at optical frequencies) and given by
In the case of dipolar materials (orientational polarization), we cannot use the simple Lorentz local field approximation. That is, the Clausius-Mossotti equation does not work with dipolar dielectrics and the calculation of the local field is quite complicated.
Table 1 summarizes the various polarization mechanisms and the corresponding static (or very low frequency) dielectric constant, and gives typical examples where one mechanism dominates over others.
Table 1
Typical examples of polarization mechanisms.
1. Problem: Electronic polarizability of non-polar gases
The electronic polarizability of the Ar atom is 1.7 × 10-40 F m2. What is the static dielectric constant of Ar gas at 1 atmosphere at room temperature (300 K)?
Solution
To calculate εr we need the number of Ar atoms per unit volume, N. If P is the pressure, V is the volume and N′ is the total number of atoms, then the ideal gas law is
PV = (N′/NA)RT
where R is the gas constant and T is the absolute temperature and N′/N is the number of moles of gas. Then, P = NkT where N = N ′/V, is the number of atoms per unit volume and k = R / NA, is the Boltzmann constant. Thus,
Using the Clausius-Mossotti equation, Equation (2), gives the same result because when Nαe is small as in the case of gases, the Clausius-Mossotti equation simplifies to Equation (1). The reader can verify this by expanding Equation (2) in a series in terms of (Nαe) and neglecting terms greater than the linear term. The dielectric constant of most gases is small for one major reason. The number of atoms or molecules per unit volume N is very small compared with the number of atoms or molecules in the liquid and solid states. Generally the dielectric constant of most nonpolar gases (including air) can be takes as 1, the same as vacuum except at very high pressures.
2. Problem: Electronic polarizability of a van der Waals solid
The electronic polarizability of the Ar atom is 1.7 × 10-40 F m2. What is the static dielectric constant of solid Ar (an FCC crystal below 84 K) if its density is 1.8 g cm-3?
Solution
To calculate εr we need the number of Ar atoms per unit volume N from the density d. If Mat = 39.95 g mol-1 is the relative atomic mass of Ar and NA is Avogadro's number then we have,
3. Problem: Relative permittivity of ionic crystals
Consider a CsCl crystal which has the CsCl unit cell crystal structure (one Cs+–Cl- pair per unit cell) with a lattice parameter (a) of 0.412 nm. The electronic polarizability of Cs+ and Cl- ions are 3.35 × 10 -40 F m2, and 3.40 × 10-40 F m2 respectively, and the mean ionic polarizability per ion pair is 6 × 10-40 . What is the low frequency dielectric constant and that at optical frequencies?
The CsCl structure has one action (Cs+) and one anion (Cl-) in the unit cell. Given the lattice parameter a = 0.412 × 10-9m, number of ion pairs Ni per unit volume is
At high frequencies, that is near optical frequencies, the ionic polarization is too sluggish to allow ionic polarization to contribute to εr. Thus, εrop, relative permittivity at optical frequencies, is given by
Note that experimental values are εr = 7.20 at low frequencies and εrop = 2.62, very close to calculated values.
4. Problem: Dielectric constant of water (a dipolar liquid)
Given the static dielectric constant of water as 80, its density as 1 g cm-3, calculate the permanent dipole moment p0 per water molecule assuming that it is the orientational polarization of individual molecules that gives rise to the dielectric constant. Use both the simple relationship in Equation (1) and also the Clausius-Mossotti equation and compare your results with the permanent dipole moment of the water molecule which is 6.1 × 10-30C m.
Solution
We first need the number of H2O molecules per unit volume. The molecular mass, Mmol is 18 × 10-3 kg mol-1, its density d is 103kg m-3. The number of H2O molecules per unit volume Nd is
This is three times greater than the actual permanent dipole moment of H2O (∼ 6 × 10-30 C m). On the other hand, if we use the Clausius-Mossotti equation we find p0 = 3.1 × 10-30 C m, which is half the actual permanent dipole moment of H2O. Both are unsatisfactory calculations. The reasons for the differences are two fold. First is that the individual H2O molecules are not totally free to rotate. In the liquid, H2O molecules cluster together through hydrogen bonding so that the rotation of individual molecules is then limited by this bonding. Secondly, the local field can neither be totally neglected nor taken as the Lorentz field. A better theory for dipolar liquids is based on the Onsager theory which is beyond the scope of this document. Interestingly, if we use the actual p0 = 6.1 × 10-30 C m in the Clausius-Mossotti equation, then εr turns out to be negative, which is nonsense.
USEFUL DEFINITIONS
Avogadro's number (NA) is the number of atoms in exactly 12 grams of Carbon-12. It is 6.022 × 1023. Since atomic mass is defined as 1/12 of the mass of the carbon-12 atom, NA number of atoms of any substance has a mass equal to the atomic mass, Mat, in grams.
Boltzmann’s constant k is the gas constant per atom or per molecule, that is, the gas constant divided by Avogadro’s number (k = R/NA); k = 1.38 × 10-23 J K-1. (3/2kT is the mean kinetic energy associated with the translational motions of gas molecules in a gas cylinder at temperature T).
Clausius-Mossotti equation relates the dielectric constant (εr), a macroscopic property, to the polarizability (α), a microscopic property.
Dielectric is a material in which energy can be stored by the polarization of the molecules. It is a material that increases the capacitance or charge storage ability of a capacitor. Ideally it is a non-conductor of electrical charge so that an applied field does not cause a flow of charge but instead a relative displacement of opposite bound charges and hence polarization of the medium.
Dipolar (orientational) polarization arises when randomly oriented polar molecules in a dielectric are rotated and aligned by the application of a field so as to give rise to a net average dipole moment per molecule. In the absence of the field the dipoles (polar molecules) are randomly oriented and there is no average dipole moment per molecule. In the presence of the field the dipoles are rotated, some partially and some fully, to align with the field and hence give rise to a net dipole moment per molecule.
Electronic polarization is the displacement of the electron cloud of an atom with respect to the positive nucleus. Its contribution to the relative permittivity of a solid is usually small.
Ionic polarization is the relative displacement of oppositely charged ions in an ionic crystal that results in the polarization of the whole material. Typically ionic polarization is important in ionic crystals below the infrared wavelengths.
Polarization is the separation of positive and negative charges in a system so that there is a net electric dipole moment per unit volume.
Relative permittivity (εr) or the dielectric constant of a dielectric is the fractional increase in the stored charge per unit voltage on the capacitor plates due to the presence of the dielectric between the plates (the whole space between the plates is assumed to be filled). Alternatively we can define it as the fractional increase in the capacitance of a capacitor when the insulation between the plates is changed from vacuum to a dielectric material keeping the geometry the same.
Valence electrons are those electrons in the outer shell of an atom. As they are the farthest away from the nucleus, they are the first electrons involved in atom-to-atom interactions.
Important Note: This article was originally written by Safa Kasap. He reserves all rights. Use this article only for educational purpose. The document can be obtained at the author`s website.
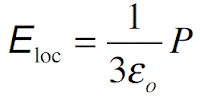
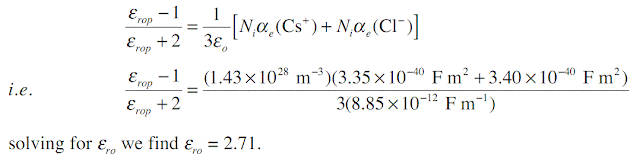
It is so easy.... Thank you
ReplyDelete