Complex Analysis: #16 The Calculus of Residues
So this is a formula for the residue of a function with a pole at a.
A rather special case is the following. Let us assume that G ⊂ ℂ is a region, and g, h are both analytic functions defined on G. Assume that a ∈ G is a simple zero of h. (That is h(a) = 0, but h'(a) ≠ 0.) Assume furthermore that g(a) ≠ 0. Then let f = g/h. (Note that a function such as f, which is defined to be the ratio of two analytic functions, is called a rational function.) Therefore f is meromorphic in G. What is the residue of f at a? Writing g and h as power series around a, we have
Of course, going in the other direction, if a is a zero of g and h(a) ≠ 0, then the residue of f at a is simply zero. This is trivial.
Theorem 35 (The Residue Theorem)
Let the function f be defined and analytic throughout the region G ⊂ ℂ, except perhaps for a set S ⊂ G of isolated, not removable singularities. Let Ω be a cycle in G which avoids all these singularities and which is such that the winding number of Ω around all points of the compliment of G is zero. Then only finitely many points of S have non-vanishing index with respect to Ω and we have the residue formula
Proof
Nothing is lost if we assume that Ω simply consists of a single closed path γ. So it is contained in a compact disc in ℂ which must contain all points of ℂ having a non-vanishing index with respect to γ. If there were infinitely many such points, then they must have an accumulation point, which must lie in the compliment of G. But such a point has index zero with respect to γ. Since that point does not lie on γ, it must have a neighborhood which contains only points with index zero with respect to γ. Thus we have a contradiction. The residue theorem now follows from Cauchy’s theorem (theorem 26).

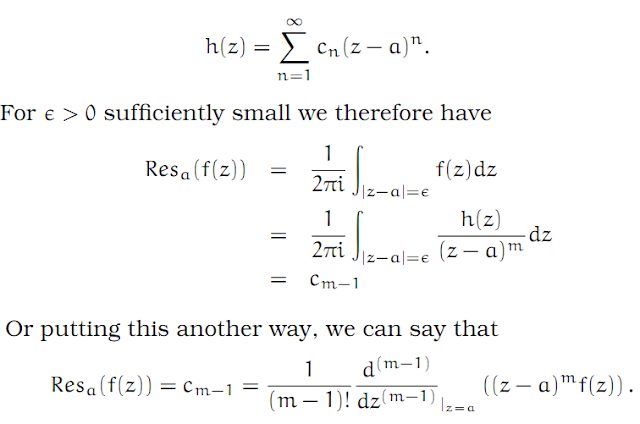


Theorem 35 is pretty rad.
ReplyDelete