Complex Analysis: #18 Integrating across a Pole
Obviously this is nonsense, since the integrals from −1 to 0, and from 0 to 1 of the function 1/x diverge. Specifically, for 0 < ∈ < 1 we have
Thus, if we agree to abandon the principles we have learned in the analysis lectures, and simply say that
then we have the Cauchy principle value of the integral, and we see that in this case it is simply zero. One could make an important-looking definition here, but let us confine our attention to integrals along closed intervals [a, b] ⊂ ℝ of complex-valued functions, where there might be poles of the function in the given interval. Assume for the moment there is a single pole at the point p ∈ (a, b). Then we will define the principle value of the integral (if it exists) to be
Then the generalization to having a finite number of poles of f along the interval (but not at the endpoints) is clear.
Theorem 38
Let R be a rational function, defined throughout ℂ (together with it’s poles). Assume that it has a zero at infinity, so that there can only be finitely many poles. Let p1 < . . . < pm be the poles of R which happen to lie on ℝ. Assume that each of these poles is simple; that is, of order 1. We distinguish two cases:
- If R has a simple zero at infinity (that is, of order 1), then we take f(z) = R(z)eiz.
- Otherwise, R has a pole of order at least 2 at infinity, and in this case we take f(z) = R(z).
Then we have
Proof
In either case, we can have only finitely many poles of the function f; therefore only finitely many poles along the real number line. Let γδ be the path along the real number line from −∞ to ∞, but altered slightly, following a semi-circle of radius δ above each of the poles on the real line. Furthermore, δ is sufficiently small that no other pole of f is enclosed within any of the semi-circles. Then, according to our previous theorems, we have
To simplify our thoughts, let us first consider the case that there is only one single pole p ∈ ℝ on the real number line. And to simplify our thoughts even further, assume that p = 0. Then we have the path γδ coming from −∞ to −δ, then it follows the path δeiπ(1−t), for t going from 0 to 1, and then finally it goes straight along the real number line from δ to ∞.
Let us now consider the Laurent series around 0. We can write
say. But then we can just define the new function g throughout ℂ (leaving out the finite set of poles of f) by the rule
Obviously g has no pole at 0, but otherwise it has the same set of poles as the original function f. Since the function c−1/z is analytic at all these other poles, the residue of g is identical with that of f around each of these poles. Therefore
Now, to get the principle value of the integral for f, we use the path γδ, but we must remove the semi-circle part of it. That is, let





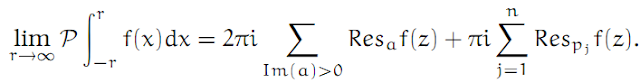





No comments:
Post a Comment
If it's a past exam question, do not include links to the paper. Only the reference.
Comments will only be published after moderation