Two sources S1 and S2 of sound are situated 80 cm apart in air, as shown in Fig. 5.1. The frequency of vibration can be varied. The two sources always vibrate in phase but have different amplitudes of vibration.

Question 13

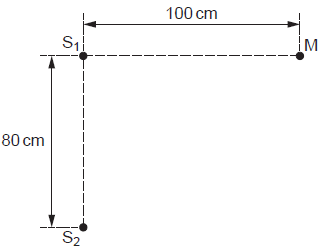
Two sources S1 and S2 of sound are situated 80 cm apart in air, as shown in Fig. 5.1.

Fig. 5.1

The frequency of vibration can be varied. The two sources always vibrate in phase but have different amplitudes of vibration.

A microphone M is situated a distance 100 cm from S1 along a line that is normal to S1S2.

As the frequency of S1 and S2 is gradually increased, the microphone M detects maxima and minima of intensity of sound.

(a) State the two conditions that must be satisfied for the intensity of sound at M to be

zero. [2]

(b) The speed of sound in air is 330 m s^-1.

The frequency of the sound from S1 and S2 is increased. Determine the number of

minima that will be detected at M as the frequency is increased from 1.0 kHz to 4.0 kHz. [4]

Reference: Past Exam Paper – June 2009 Paper 21 Q5

Solution:

(a)

{The intensity of the sound at M is zero when destructive interference occurs.}

Condition 1:    EITHER the phase difference is π rad / 180° (anti-phase)

OR path difference (between the waves from S₁ and S₂) is ½ λ / (n + ½) λ 

Condition 2:    EITHER the waves have the same amplitude / intensity at M

{Destructive interference occurs and the resultant amplitude is zero. 

Let amplitude of each wave be A. For destructive interference, resultant amplitude = A – A = 0

BUT if the amplitude of one wave is A and the amplitude of the other is 0.5A. Resultant amplitude = A – 0.5A = 0.5A. The resultant amplitude is NOT zero.

So, for destructive interference, the waves should have the SAME amplitude.}

OR the ratio of amplitudes is 1.28 / ratio of intensities is 1.28²

{From Pythagoras’ theorem, the distance S₂M is 128 cm.

Note that the amplitudes of the waves decrease as they travel over distances since they lose energy.

So, the ratio of amplitudes should be 128 / 100 = 1.28 such that the waves would have the same amplitude at point M (even though they are emitted at different amplitudes at S₁ and S₂).

Intensity ∝ (amplitude)²

So, the ratio of intensities = (ratio of amplitudes)² = 1.28² }

(b)

Path difference between the waves from S₁ and S₂ = (128 – 100 =) 28 cm

{v = f λ

when frequency = 1 kHz, wavelength = 330 / 1000 = 0.33 m = 33 cm

when frequency = 4kHz, wavelength = 330 / 4000 = 0.0825 m = 8.25 cm}

The wavelength changes from 33 cm to 8.25 cm {as the frequency is increased}

{Condition for destructive interference:

path difference = (n + ½) λ

(n + ½) λ = 28

Wavelength λ = 28 / (n + ½)

When n = 0, λ = 56 cm           {but this is outside the range}

When n = 1, λ = 18.7 cm        {within range}

When n = 2, λ = 11.2 cm        {within range}

When n = 3, λ = 8.0 cm          {but this is outside the range}

Minima will be detected when λ = (56cm,) 18.7cm, 11.2cm, (8.0cm).

 
So, there are 2 minima.           {that are within the range}