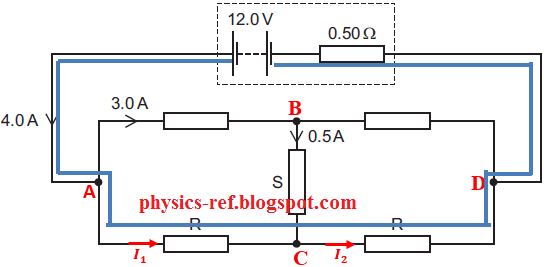
Question 13
The circuit shown contains a resistor S that is neither
in series nor in parallel with the other resistors.
Kirchhoff’s laws can be used with the data in the diagram
to deduce the resistance of each of the two identical resistors labelled R.
What is the resistance of each resistor R?
A 3.0 Ω B 4.0 Ω C 4.8 Ω D 5.0 Ω
Reference: Past Exam Paper – November 2017 paper 12 Q37
Solution:
Answer: B.
This question needs to be
tackled from first principles. Data that can be easily found should be included
in the diagram.
Using Kirchhoff’s first
law, the currents flowing in the different resistors can be found.
At any junction, sum of
currents entering = sum of currents leaving
At junction A, I1
+ 3.0 = 4.0 giving I1
= 1.0 A
At junction C, I2
= I1 + 0.5 = 1.0 + 0.5 = 1.5 A
The current coming out of
the battery is the same current that goes back into the battery. So, the
current flowing through the internal resistance of the battery is 4.0 A.
Using Kirchhoff’s second
law, the sum of p.d. across any loop should be equal to the e.m.f. in the circuit.
Consider the loop drawn in
blue on the diagram.
1R + I2R + (4.0×0.5) = 12
R (I1 + I2)
+ 2 = 12
R = (12 – 2) / (1.0 + 1.5) = 10 / 2.5 = 4 Ω


so helpful omg thank you. I just want to appreciate all the hardwork you guys put into this site
ReplyDeleteSO BASICALLY RESISTOR S IS IGNORED IN THIS QUESTION??
ReplyDeleteyes, since the loop we have chosen does not include S.
Deleteif someone chooses another loop that contain S, they would need to include it (while another resistor(s) would be ommited them)
Aslamualikum! I am confused that how is t even possible that potential difference across two resistors labelled R equalts to the terminal potential difference as there would also be potential difference across resistor S
ReplyDeleteWslm. S is not even in the loop considered.
DeleteFrom Kirchhoff's law, the sum of p.d. in any loop is equal to the sum of emf in that loop.
If we had considered another loop containing S, then the e.m.f. would be divided among the components considered.
It is important to observe that no loop contains both resistors and S at the same time.