Physics 9702 Doubts | Help Page 101
Question 518: [Kinematics]
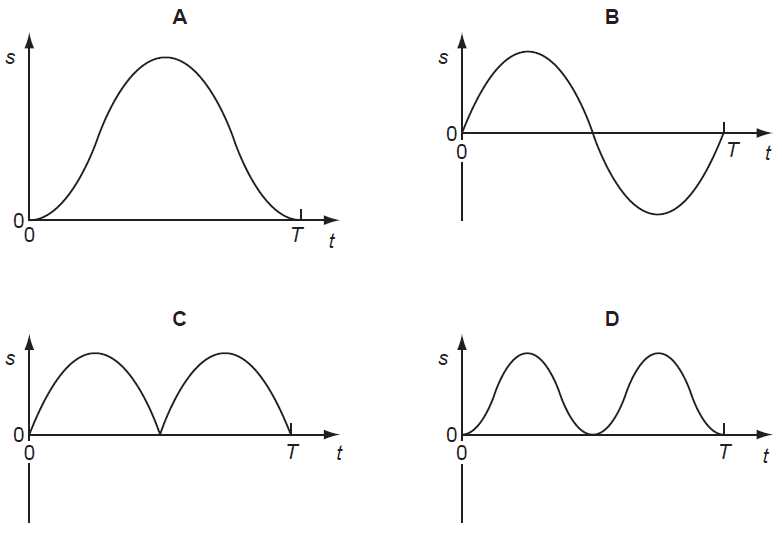
Graph shows how the velocity v of an object moving in straight line varies over time t = 0 to t = T.
Which graph represents displacement s of the object in the time t = 0 to t = T?
Reference: Past Exam Paper – June 2012 Paper 12 Q7
Solution 518:
Answer: A.
The object moves in a straight line.
Velocity is a vector, so a positive
value would indicate that the object is moving in one direction along the
straight line (e.g. forward) and a negative value would indicate motion in the
opposite direction (e.g. backward).
From a velocity-time graph, the
displacement is obtained by the area under the graph. Displacement is also a
vector, so when the velocity is positive (curve is above the t-axis), the
displacement increases and when the velocity is negative (curve is below the
t-axis), the displacement decreases.
Interpretation
of the velocity-time graph of the object:
Velocity v increases until it
reaches a maximum value, and then decreases back to zero (while still having
positive values). The increase and decrease are not constant (since graphs are
not straight line, so acceleration is not constant). The motion till here is away
from the point of start. Thus, the maximum displacement is at this point.
Then, the velocity increases again
but now the object is moving in the opposite direction since the velocity has
negative values. Since it is mentioned that the motion is in a straight line,
the object is now moving towards the point of start. The velocity
reaches a maximum value (while still being negative) and then decreases again
until it becomes zero. The object has reached its initial point of start.
Question 519: [Work, Energy and Power]
Car travelling on a level road at steady 20 m s–1 against a constant resistive force develops a power of 40 kW.
What is magnitude of the resistive force?
A 200 N B 800 N C 2000 N D 4000 N
Reference: Past Exam Paper – November 2013 Paper 11 & 12 Q18
Solution 519:
Answer: C.
Since the car travels at a steady speed, the net force on the car is zero.
So, the resistive force on the car is equal to the force provided by the engine
of the car.
Power = Work Done / Time = Force x
distance / time = Force x speed
Force = 40 000 / 20 = 2 000 N
Question 520: [Units]
Unit of resistivity, expressed in terms of base units, is given by
kg x3 y–2 z–3
.
Which base units are x, y and z?
x y
z
A ampere metre secondB metre ampere second
C metre second ampere
D second ampere metre
Reference: Past Exam Paper – June 2013 Paper 12 Q2
Solution 520:
Answer: B.
Resistance R = ρL / A
So, resistivity ρ = RA / L
But, from Ohm’s law, resistance R = V
/ I. Also, power P = VI, giving V = P / I
So, resistance may be written as R =
P / I2.
Power P = Work done / time = (Force
x Distance) / time
Power P = (mass x acceleration x
Distance) / time.
Units of power P: kg ms-2
m s-1 = kg m2 s-3
So, units of resistance, R: kgm2s-3A-2 and units of resistivity ρ (= RA / L): kgm2s-3A-2 m2 m-1 = kgm3s-3A-2
Question 521: [Work, Energy and Power]
Kinetic energy of vehicle of mass 1000 kg is 4.5 × 105 J. It is braked with total constant braking force of 6000 N.
What will be its stopping distance?
A 37 m B 75 m C 150 m D 300 m
Reference: Past Exam Paper – November 2011 Paper 12 Q16
Solution 521:
Answer: B.
Work done to stop vehicle = Kinetic
energy = 4.5x105J
Work done = Force x distance
Distance s = Work done / Force =
(4.5x105) / 6000 = 75m
Question 522: [Current of Electricity]
(a) For a cell, explain terms
(i) electromotive force (e.m.f.)
(ii) internal resistance
(b) Circuit of Fig shows two batteries A and B and a resistor R
connected in series.
Battery A has e.m.f. of 3.0 V and
internal resistance of 0.10 Ω. Battery B
has e.m.f. of 12 V and internal resistance of 0.20
Ω. Resistor R has resistance of 3.3 Ω.
(i) Apply Kirchhoff’s second law to
calculate current in the circuit
(ii) Calculate power transformed by
battery B
(iii) Calculate total energy lost
per second in resistor R and the internal resistances
(c) Circuit of Fig may be used to store energy in
battery A. Suggest how answers in (b) support this statement
Reference: Past Exam Paper – June 2011 Paper 22 Q5
Solution 522:
(a)
(i) The electromotive force (e.m.f)
of a cell is the energy converted from chemical to electrical when charge flows
through a cell or round a complete circuit.
(ii) The internal resistance of a
cell is (the resistance of a cell) causing loss of voltage or energy loss in
the cell.
(b)
(i)
{From Kirchhoff’s second
law, it is known that the algebraic sum of the potential differences in a
circuit loop must be zero. In other words, the sum of p.d. across the different
components that provide some sort of resistance should be equal to the overall
e.m.f. in the circuit.
Current flows from the
positive terminal of a battery. If we look at the circuit, it can be seen that
the current flowing from the 2 batteries oppose each other. However, in a
circuit, current can only flow in one direction. Therefore, in this case, we
find the overall e.m.f. that provide a current in ONE direction. This is done
by subtracting the e.m.f.s of the batteries. Current would flow from the
battery having the higher e.m.f.
The difference in e.m.f.s
would be equal to the sum of p.d. across the resistances (including internal
resistances).}
EB – EA = I (R
+ rB + rA)
12 – 3 = I (3.3 + 0.1 + 0.2)
I = 2.5A
(ii) Power = EBI =
12(2.5) = 30W
(iii)
(Total resistance, R =
3.3+0.2+0.1 = 3.6. Overall emf, V = 12 – 3 = 9)
Either P = I2R = (2.5)2x3.6
= 22.5Js-1
Or P = V2/R = 92/3.6
= 22.5Js-1
Or P = VI = 9 x 2.5 = 22.5Js-1
(c) The power supplied from cell B is greater than
the energy lost per second in the circuit.



for sulution 552 here, part bii why cant I use the formula of P=V^2/R
ReplyDeleteFor cells / batteries,
DeletePower P = EI
where E is the e.m.f of thee battery and I the current it produces. I is the total current in the circuit.
For resistors,
P = VI = I^2R = V^2 / R
where V is the p.d. across the resistor, I the current through it and R the resistance of the resistor. Current I has be different through different resistors in a circuit (if the resistors are in parallel)
Thankyou so much for the help, what a great website. God Bless You
ReplyDeleteFor solution 520, why can't we use V=IR and make R the subject, R=V/R
ReplyDeleteNow for the units of V, we use energy/charge?
Of course you can. If you did it, try to show the derivation below. We'll see which one is quickest, easiest, ...
DeleteI only derived it in one way. There may be others.
For units of resistivity,
DeleteR=pL/A
p=RA/L
For the units of resistances, we use R=V/I. V is energy/charge. Units of voltage will be kgm^2s^-1C^-1
I=Q/T, therefore q=As
Kgm^2s^-1A^-1s^-1
You'll need to memorize the units of voltage. The method uses simple units, ...
DeleteWell, as long as you are find with it, ...