• Physics 9702 Doubts | Help Page 61

Question 345: [Radioactive Decay]
The nuclide ²²⁶₈₈Ra occurs in appreciable quantities in a mineral of great geological age despite the fact that its half-life is only a very small fraction of the age of the mineral. This is because
A the radioactive decay of ²²⁶₈₈Ra is exponential and the activity can never become zero.
B ²²⁶₈₈Ra is constantly being formed by the decay of a longer-lived isotope.
C the mineral is constantly being subjected to neutron bombardment from the centre of the Earth, forming more ²²⁶₈₈Ra.
D the concentration of ²²⁶₈₈Ra is constantly being regenerated by radioactive fall-out from the atmosphere.
E the rock surrounding the ²²⁶₈₈Ra slows down the escape of the alpha-particles and gamma-rays.

Reference: Past Exam Paper – N79 / II / 36 & J82 / II / 38 & J87 / I / 27



Solution 345:
Answer: B.
The correct answer should be reasonable and relevant, based on the simple theories learned in the course.

Even if choice A may be true, the ²²⁶₈₈Ra would be present in only a scarce amount.

The only correct and reasonable choice is that the ²²⁶₈₈Ra is constantly being formed by the decay of a longer-lived isotope.









Question 346: [Nuclear Physics]
The isotope ²²⁶₈₈Ra decays into ²²²₈₆Rn with the emission of an α-particle and a γ-ray photon of frequency υ.
The principle of conservation of energy is expressed in the decay equation
A 88 = 86 + 2
B 226 = 222 + 4
C [m_Ra – m_Rn] c² = hυ
D ½ m_Rn u_Rn² = hυ + ½ m_α u_α²
E [m_Ra – (m_Rn + m_α] c² = hυ + ½ m_α u_α² + ½ m_Rn u_Rn²

Reference: Past Exam Paper – N80 / II / 39



Solution 346:
Answer: E.
The equation for the decay is

²²⁶₈₈Ra             - - - >   ²²²₈₆Rn             +          ⁴₂α        +          γ

Choice A is an equation for the proton number while choice B equates the mass number without considering the γ-ray. [A and B are incorrect]

The ²²⁶₈₈Ra, ²²²₈₆Rn and ⁴₂α all have some masses while the γ-ray, which is an EM wave, has no mass.

After the decay, the ²²²₈₆Rn and ⁴₂α emitted would move with some energy – kinetic energy. Their kinetic energy would be provided by the mass defect between the parent nucleus (²²⁶₈₈Ra) and the daughter nucleus (²²²₈₆Rn) along with the alpha particle emitted.

The energy due to this mass defect is [m_Ra – (m_Rn + m_α] c²

This energy is converted to the kinetic energy of the ²²²₈₆Rn and ⁴₂α. Part of that energy is also used to liberate the γ-ray photon.

Energy of γ-ray photon = hυ
Kinetic energy of ²²²₈₆Rn = ½ m_Rn u_Rn²
Kinetic energy of ⁴₂α = ½ m_α u_α²

Only choice E accounts for all these energies.











Question 347: [Current of Electricity > Kirchhoff’s law]
Diagram shows a circuit in which the battery has negligible internal resistance.

What is the value of the current I?
A 1.0 A                       B 1.6 A                       C 2.0 A                       D 3.0 A

Reference: Past Exam Paper – November 2003 Paper 1 Q31



Solution 347:

Answer: A.

Total resistance in circuit = [1/6 + 1/3]^-1 + 2 = 2 + 2 = 4Ω

Total current supplied by battery = V / R = 12 / 4 = 3.0A

EITHER

2 loops can be seen in the circuit.

Loop 1: battery – 6.0 Ω resistor – 2.0 Ω resistor

Loop 2: battery – 3.0 Ω resistor – 2.0 Ω resistor

From Kirchhoff’s law, the sum of potential difference across the components in each loop is the same (and equal to 12V here).

Consider loop 1:

The total current of 3.0A flows through the 2.0 Ω resistor.

p.d. across 2.0 Ω resistor = 3.0 (2.0) = 6.0V

Therefore, the p.d. across the 6.0 Ω resistor = 12 – 6 = 6.0V

Current I through the 6.0 Ω resistor = V / R = 6.0 / 6.0 = 1.0 A

OR

The total current of 3.0 A would split at the junction of the 2 resistors in parallel. From Ohm’s law (V = IR), the current is inversely proportional to the resistance. That is, when the resistance is big, the current is small.

Since the resistance 6.0 Ω resistor is twice that of the 3.0 Ω resistor, the current I through the 6.0 Ω resistor would be half that through the 3.0 Ω resistor.

So, current in 6.0 Ω resistor = 1.0A and current in 3.0 Ω resistor = 2.0A.

Total current = 1.0 + 2.0 = 3.0A

Question 348: [Electromagnetism > Oscillations]

Aluminium sheet is suspended from an oscillator by means of a spring, as illustrated.

Electromagnet is placed a short distance from centre of the aluminium sheet.

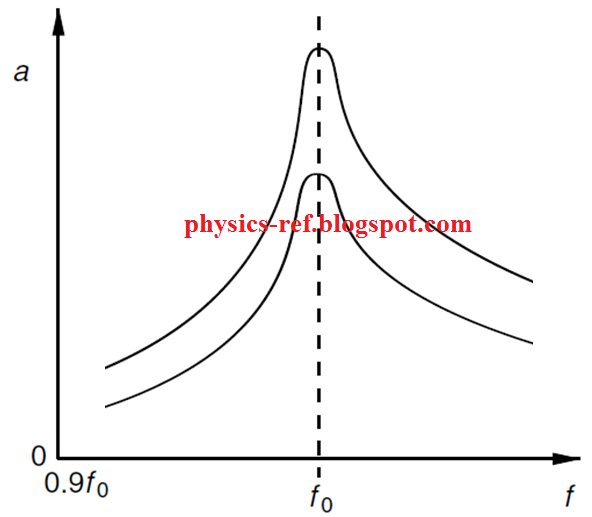
Electromagnet is switched off and frequency f of oscillation of the oscillator is gradually increased from a low value. Variation with frequency f of amplitude a of vibration of the sheet is shown.

A peak on graph appears at frequency f₀.

(a) Explain why there is a peak at frequency f₀.

(b) Electromagnet is now switched on and frequency of the oscillator is again gradually increased from a low value. On Fig, draw a line to show variation with frequency f of the amplitude a of vibration of the sheet.

(c) Frequency of oscillator is now maintained at a constant value. Amplitude of vibration is found to decrease when current in the electromagnet is switched on.

Use laws of electromagnetic induction to explain this observation.

Reference: Past Exam Paper – June 2003 Paper 4 Q3



Solution 348:

(a) The frequency f₀ is the natural frequency of the spring (system). This frequency is at the driver frequency.

{So, resonance occurs.}

(b) The line drawn should have the amplitude less (than the graph shown) at all frequencies. The peak should be flatter with the peak being at f0 or slightly below f₀.

(c) The (aluminium) sheet cuts the magnetic flux/field, so currents / e.m.f. are induced in the (metal) sheet. These current dissipate energy. So, less energy is available for the oscillations. So, the amplitude is smaller.