• Physics 9702 Doubts | Help Page 59

Question 335: [Matter > Elasticity]
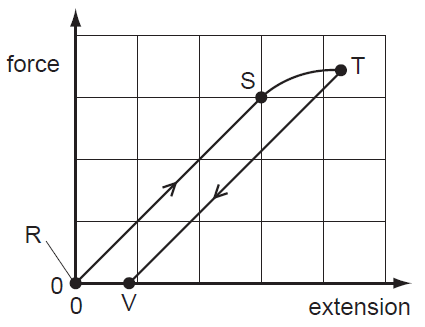
A long, thin metal wire is suspended from fixed support and hangs vertically. Masses are suspended from its lower end.
Load on the lower end is increased from zero and then decreased again back to zero.
Diagram shows the force-extension graph produced.

Where on graph would the elastic limit be found?
A anywhere between point R and point S
B beyond point S but before point T
C exactly at point S
D exactly at point T

Reference: Past Exam Paper – June 2011 Paper 11 Q20



Solution 335:
Answer: B.
The elastic limit is beyond the limit of proportionality.

Up to the limit of proportionality, the force is extension is proportional to the force – that is, the graph is linear. The limit of proportionality is exactly at S, so the elastic limit should be beyond S. [A and C are incorrect]

Up to the elastic limit, the wire would still behave elastically – that is, it regains its original shape when the deforming force is removed. Point T is therefore beyond the elastic limit since plastic deformation occurs when the force is reduced to zero. [D is incorrect]









Question 336: [Matter > Solids]
Stress-strain graphs for four different materials are shown below.
Which diagram shows stress-strain graph for a ductile metal?

Reference: Past Exam Paper – June 2013 Paper 11 Q22



Solution 336:
Answer: A.
Material that undergo plastic deformation before breaking are said to be ductile. So, the graph should go beyond the elastic limit.

Since it is for a metal, it should obey Hooke’s law up to some point – that is, a part of the graph should be a straight line. Then, beyond the limit of proportionality, the graph is no longer linear and beyond the elastic limit, plastic deformation occurs. [A is correct and C is incorrect]

Graph B is that of an amorphous solid, such as glass. It does not shown plastic behaviour (it is brittle) but instead would break when some stress is applied to it.

Graph D is that of a polymer (such as rubber). When the stress is removed, even if the shape of the graph is not the same, the material would still regain its original shape.









Question 337: [Nuclear Physics > Scattering experiment]

α-particle scattering experiment provided evidence for existence of a nuclear atom.

(a) State what could be deduced from fact that

(i) most α-particles were deviated through angles of less than 10°

(ii) a very small proportion of the α-particles was deviated through angles greater than 90°

(b) Fig shows path AB of an α-particle as it approaches and passes by a stationary gold nucleus.

On Fig, draw lines (one in each case) to complete the paths of α-particles passing by the gold nucleus when the initial direction of approach is

(i) along line CD,

(ii) along line EF.

Reference: Past Exam Paper – November 2004 Paper 2 Q7



Solution 337:

(a)

(i) The nucleus is small in comparison to the size of the atom.

(ii) The nucleus is massive / heavy / dense and is charged

(b)

(i) The line should be a symmetrical path and the deviation correct with respect to the position of the nucleus. The deviation should be less than in path AB

(ii) The deviation is greater than 90° and in the correct direction

Question 338:

Derive the escape speed.

Solution 338:

The gravitational potential energy of an object at a point is defined as the energy required to bring the object from infinity to that point.

The gravitational potential energy of a mass m on Earth is

– GMm / R

where M = mass of Earth, R = radius of Earth.

To bring an object from the surface of Earth to infinity, the same amount of energy is required.

Therefore, to launch a rocket of mass m from the Earth’s surface so that it escapes completely from the gravitational attraction of the Earth, the rocket must take off from Earth with

Kinetic energy ≥ GMm / R

½ mv² ≥ GMm / R

v ≥ √(2GM / R)

The least speed required, i.e. v = √(2GM / R), for an object to escape completely from the Earth and never to return is known as the escape speed from the Earth.

Escape speed from the Earth = √(2GM / R)
But GM = gR²,           [from g = GM / R²]
Escape speed, v = √(2gR² / R) = √(2gR) = √[2 (9.81) (6.4x10⁶)] = 11.2 kms^-1


Reference: “Pacific Physics A Level” Volume 1, by POH LIONG YONG, pg 238 - 239