Linear Algebra: #19 "Classical Groups" often seen in Physics
- The orthogonal group O(n): This is the set of all linear mappings f : ℜn → ℜn such that <u, v> = <f(u), f(v)>, for all u, v ∈ ℜn. We think of this as being all possible rotations and inversions (Spiegelungen) of n-dimensional Euclidean space.
- The special orthogonal group SO(n): This is the subgroup of O(n), containing all orthogonal mappings whose matrices have determinant +1.
- The unitary group U(n): The analog of O(n), where the vector space is n-dimensional complex space ℂn. That is, <u, v> = <f(u), f(v)>, for all u, v ∈ ℂn.
- The special unitary group SU(n): Again, the subgroup of U(n) with determinant +1.
Note that for orthogonal, or unitary mappings, all eigenvalues — if they exist — must have absolute value 1. To see this, let v be an eigenvector with eigenvalue λ. Then we have
Since v is an eigenvector, and thus v ≠ 0, we must have |λ| = 1.
We will prove that all unitary matrices can be diagonalized. That is, for every unitary mapping ℂn → ℂn, there exists a basis consisting of eigenvectors. On the other hand, as we have already seen in the case of simple rotations of 2-dimensional space, “most” orthogonal matrices cannot be diagonalized. On the other hand, we can prove that every orthogonal mapping ℜn → ℜn, where n is an odd number, has at least one eigenvector. [For example, in our normal 3-dimensional space of physical reality, any rotating object — for example the Earth rotating in space — has an axis of rotation, which is an eigenvector.]
- The self-adjoint mappings f (of ℜn
→ ℜn
or ℂn
→ ℂn) are such that <u, f(v)> = <f(v), u>, for all u, v in ℜn
or ℂn, respectively. As we will see, the matrices for
such mappings are symmetric in the real case, and Hermitian in the complex
case. In either case, the matrices can be diagonalized. Examples of Hermitian
matrices are the Pauli spin-matrices:
We also have the Lorentz group, which is important in the Theory of Relativity. Let us imagine that physical space is ℜ4, and a typical point is v = (tv, xv, yv, zv). Physicists call this Minkowski space, which they often denote by M4. A linear mapping f : M4 → M4 is called a Lorentz transformation if, for f(v) = (tv*, xv*, yv*, zv*), we have
- − (tv*)2 + (xv*)2 + (yv*)2 + (zv*)2 = − tv2 + xv2 + yv2 + zv2 for all v ∈ M4, and also the mapping is “time-preserving” in the sense that the unit vector in the time direction, (1, 0, 0, 0) is mapped to some vector (t*, x*, y*, z*), such that t* > 0.
The Poincare group is obtained if we consider, in addition, translations of Minkowski space. But translations are not linear mappings, so I will not consider these things further in this lecture.


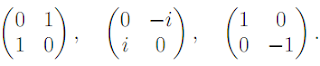
No comments:
Post a Comment
If it's a past exam question, do not include links to the paper. Only the reference.
Comments will only be published after moderation