Linear Algebra: #15 Why is the Determinant Important?
- The transformation formula for integrals in higher-dimensional spaces.
This is a theorem which is usually dealt with in the Analysis III lecture. Let G ⊂ ℜn be some open region, and let f : G → ℜ be a continuous function. Then the integral
has some particular value (assuming, of course, that the integral converges). Now assume that we have a continuously differentiable injective mapping φ : G → ℜn and a continuous function F : φ(G) → ℜ. Then we have the formula
Here, D(φ(x)) is the Jacobi matrix of φ at the point x.
This formula reflects the geometric idea that the determinant measures the change of the volume of n-dimensional space under the mapping φ.
If φ is a linear mapping, then take Q ⊂ ℜn to be the unit cube: Q = {(x1, . . . , xn) : 0 ≤ xi ≤ 1, ∀i}. Then the volume of Q, which we can denote by vol(Q) is simply 1. On the other hand, we have vol(φ(Q)) = det(A), where A is the matrix representing φ with respect to the canonical coordinates for ℜn. (A negative determinant — giving a negative volume — represents an orientation-reversing mapping.) - The characteristic polynomial.
Let f : V → V be a linear mapping, and let v be an eigenvector of f with f(v) = λv. That means that (f − λIn)(v) = 0; therefore the mapping (f − λIn) : V → V is singular. Now consider the matrix A, representing f with respect to some particular basis of V. Since λIn is the matrix representing the mapping λIn, we must have that the difference A − λIn is a singular matrix. In particular, we have det(A − λIn) = 0.
Another way of looking at this is to take a “variable” x, and then calculate (for example, using the Leibniz formula) the polynomial in x
P(x) = det(A − xIn).
This polynomial is called the characteristic polynomial for the matrix A. Therefore we have the theorem:
Theorem 41
The zeros of the characteristic polynomial of A are the eigenvalues of the linear mapping f : V → V which A represents.
Obviously the degree of the polynomial is n for an n × n matrix A. So let us write the characteristic polynomial in the standard form
P(x) = cnxn + cn−1xn−1 + · · · + c1x + c0 .
The coefficients c0, . . . , cn are all elements of our field F.
Now the matrix A represents the mapping f with respect to a particular choice of basis for the vector space V. With respect to some other basis, f is represented by some other matrix A', which is similar to A. That is, there exists some C ∈ GL(n, F) with A' = C−1AC. But we have
Therefore we have:
Theorem 42
The characteristic polynomial is invariant under a change of basis; that is, under a similarity transformation of the matrix.
In particular, each of the coefficients ci of the characteristic polynomial P(x) = cnxn + cn−1xn−1 + · · · + c1x + c0 remains unchanged after a similarity transformation of the matrix A.
What is the coefficient cn? Looking at the Leibniz formula, we see that the term xn can only occur in the product
(a11 − x)(a22 − x) · · · (ann − x) = (−1)xn − (a11 + a22 + · · · + ann)xn−1 + · · · .
Therefore cn = 1 if n is even, and cn = −1 if n is odd. This is not particularly interesting.
So let us go one term lower and look at the coefficient cn−1. Where does xn−1 occur in the Leibniz formula? Well, as we have just seen, there certainly is the term
(−1)n−1(a11 + a22 + · · · + ann)xn−1,
which comes from the product of the diagonal elements in the matrix A − xIn. Do any other terms also involve the power xn−1? Let us look at Leibniz formula more carefully in this situation. We have
Here, δij = 1 if i = j. Otherwise, δij = 0. Now if σ is a non-trivial permutation — not just the identity mapping — then obviously we must have two different numbers i1 and i2, with σ(i1) ≠ i1 and also σ(i2) ≠ i2. Therefore we see that these further terms in the sum can only contribute at most n − 2 powers of x. So we conclude that the (n − 1)-st coefficient is
cn−1 + = (−1)n−1(a11 + a22 + · · · + ann).
Definition
Let A be an n × n matrix. The trace of A (in German, the spur of A) is the sum of the diagonal elements:
tr(A) = a11 + a22 + · · · + ann.
Theorem 43
tr(A) remains unchanged under a similarity transformation.
An example
Let f : ℜ2 → ℜ2 be a rotation through the angle θ. Then, with respect to the canonical basis of ℜ2, the matrix of f is
That is to say, if λ ∈ ℜ is an eigenvalue of f, then λ must be a zero of the characteristic polynomial. That is,
λ2
− 2λ cos θ + 1 = 0.
But, looking at the well-known formula for the roots of quadratic polynomials, we see that such a λ can only exist if |cos θ| = 1. That is, θ = 0 or π. This reflects the obvious geometric fact that a rotation through any angle other than 0 or π rotates any vector away from its original axis. In any case, the two possible values of θ give the two possible eigenvalues for f, namely +1 and −1.






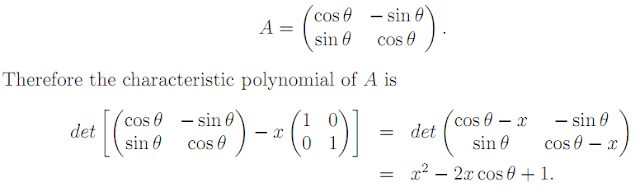
No comments:
Post a Comment
If it's a past exam question, do not include links to the paper. Only the reference.
Comments will only be published after moderation