Physics 9702 Doubts | Help Page 146
Question 721: [Matter
> Hooke’s law]
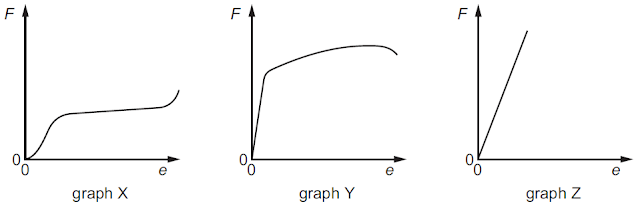
Cylindrical samples of steel, glass
and rubber are each subjected to gradually increasing tensile force F. Extensions
e are measured and graphs are plotted as shown below.
Which row correctly relates the
graphs to the materials?
steel
glass rubber
A X
Y Z
B X
Z Y
C Y
X Z
D Y
Z X
Reference: Past Exam Paper – June 2005 Paper 1 Q21 & June 2014 Paper
13 Q24
Solution 721:
Answer: D.
Graph X relates to rubber. It does
not obey Hooke’s law.
Graph Y relates to steel. It obeys
Hooke’s law until the limit of proportionality. Then, the extension is no
longer proportional to the force – plastic deformation occurs. As more force is
applied, the material will each a point where it breaks.
Graph Z relates to glass. The graph
has a steep gradient and the extension is relatively much less than the other
materials. This indicates if a force big enough is applied, the material breaks
– so, we cannot extend the graph for large values of extension.
Question 722: [Measurement]
(a) State SI base units of force.
(b) Two wires each of length l are placed parallel to each
other a distance x apart, as shown in Fig.1.
Each wire carries a current I. Currents
give rise to a force F on each wire given by
F = KI2l / x
where K is a constant.
(i) Determine SI base units of K.
(ii) On Fig.2, sketch variation with
x of F. The quantities I and l remain constant.
(iii) Current I in both of the wires
is varied.
On Fig.3, sketch variation with I of
F. The quantities x and l remain constant.
Reference: Past Exam Paper – June 2013 Paper 23 Q1
Solution 722:
(a) SI Unit of Force: kg m s–2
(b)
(i)
Units: I2: A2 l:
m x: m
{K = Fx / I2l}
Units of K: kg m s–2 A–2
(ii) The curve of the correct shape (for
inverse proportionality) should clearly be shown approaching each axis but
never touching the axis
{The graph has the same
shape as a graph of y = 1 / x. Plotting the values of x and y that are very
close to each other will show that the graph is a curve, not a straight line.
When x = 0, y = 1 / 0 = ∞ but we can’t plot a graph showing ∞, so the line should approach the
axis but never touches the axis. Similarly, when y = 0, x = 1 / 0 = ∞.}
(iii) The graph should be shown
curving upwards and through the origin
{The graph has the same
shape as a graph of y = x2.}
Question 723: [Dynamics
> Collision]
Particle of mass 2m and velocity v
strikes a wall.
The particle rebounds along same
path after colliding with the wall. The collision is inelastic.
What is a possible change in
momentum of the ball during the collision?
A mv B 2mv C
3mv D 4mv
Reference: Past Exam Paper – November 2010 Paper 12 Q9
Solution 723:
Answer: C.
Initial momentum of particle = (2m)v
= 2mv
Initial kinetic energy of particle =
½ (2m) v2 = mv2
In an inelastic collision, energy is
lost – so the kinetic energy of the particle must be less than it was before
the collision. But momentum is still conserved.
The wall is fixed (not moving), so
its initial momentum is zero.
After colliding with the wall, the
particle rebounds along same path. So, its direction has changed.
Momentum is a vector quantity, so we
need to consider its direction too.
Consider the direction towards the
wall to be positive.
Initial momentum of particle = (2m)v
= +2mv
The final momentum of the particle
needs to be negative since its direction has changed.
If the change in momentum Δm = mv,
Final momentum of particle = +2mv –
mv = +mv
The direction is still positive.
This means that the particle is still moving towards the wall after collision.
We know, from the question, that this is incorrect.
If Δm
= 2mv,
Final momentum of particle = +2mv – 2mv
= 0
This means that the particle remains
stationary after collision. This is incorrect since we know that the particle
moves in the opposite direction.
If Δm
= 3mv,
Final momentum of particle = +2mv – 3mv
= – mv
The particle moves away from the
wall. Mass of the particle = 2m, so the velocity of the particle is now –v/2 so
that the momentum = (2m) (–v/2) = – mv
Final kinetic energy of particle = ½
(2m) (v/2)2 = mv2 / 4
The energy is less than before since
this is an inelastic collision.
If Δm
= 4mv,
Final momentum of particle = +2mv – 4mv
= – 2mv
The particle moves away from the
wall. Mass of the particle = 2m, so the velocity of the particle is now –v so
that the momentum = (2m) (–v) = – 2mv
Final kinetic energy of particle = ½
(2m) (v)2 = mv2
Here, the energy is conserved, which
is incorrect for an inelastic collision.
Question 724:
[Nuclear Physics]
It was once thought that the mass of
an atom is spread uniformly through volume of the atom. When α-particles are
directed at a piece of gold foil, the results led scientists to believe instead
that nearly all the mass of the gold atom is concentrated at a point inside the
atom.
Which effect is possible only
if nearly all the mass of the gold atom is concentrated at a point?
A a few α-particles bounce back
B most α-particles are only slightly
deflected
C some α-particles pass through
without any deflection
D some α-particles are absorbed
Reference: Past Exam Paper – June 2013 Paper 11 Q39
Solution 724:
Answer: A.
We need to say which if the effects
given is ONLY possible if nearly all the mass is concentrated at one point in
the atom.
If nearly all the mass is
concentrated at a point, a few α-particles would bounce back. These are the α-particles
that collide with that point (of concentrated mass) and their direction are
reverse.
The α-particles that are slightly
deflected are due to the charges of the α-particles and that of the point being
the same (like charges repel). The reason is NOT because nearly all the mass is
concentrated at the centre. [B is incorrect]
The fact that some α-particles pass
through without any deflection is because most of the golf atom is empty space.
By passing at a relatively longer distance than the other α-particles, these α-particles
do not experience the electric repulsion sue to the charges. [C is incorrect]
The absorption of some α-particles
occurs due to nuclear reactions. This is not ONLY due to the fact that most of
the mass is concentrated at a point. [D is
incorrect]




in solution 723 isn't the final momentum = initial + change in momentum( as change in momentum = final - initial)?? please help me
ReplyDeletethe change in momentum is negative, as explained above. The values given as the choices are only the magnitudes. Only we need to take the negative.
Deleteis change in momentum = initial mom - final mom or is it equal to final mom-initial mom.
Deletefinal - initial
DeleteThen why have you used initial-final?
DeleteChange in momentum – Final momentum – Initial momentum
DeleteFinal momentum = Initial momentum + change in momentum
But since ‘change in momentum’ has a negative value, we need to take the negative.
Final momentum = Initial momentum + (–)change in momentum
Final momentum = Initial momentum – change in momentum
In question 723 where they have told to take change in momentum negative
ReplyDeletethe speed v towards the wall is given as positive.
Deleteafter bouncing, the ball would move in the opposite direction, which is thus negative.
so, the momentum changes from positive to negative. the change should therefore be negative.
Note: read the comments above