• Physics 9702 Doubts | Help Page 39

Question 241: [Waves > Diffraction]

(a) Explain what is meant by diffraction of a wave.

(b)

(i) Outline briefly an experiment that may be used to demonstrate diffraction of transverse wave.

(ii) How experiment in (i) may be changed to demonstrate diffraction of a longitudinal wave.

Reference: Past Exam Paper – November 2008 Paper 2 Q6



Solution 241:

(a)

Diffraction of a wave is the bending / spreading of the wave (into geometrical shadow) when the wave is incident at an edge / aperture / slit / (edge of) obstacle.

(b)

(i)

Examples for the apparatus:

Laser & slit / a point source & slit / lamp and slit & slit

A microwave source & slit

Water / ripple tank, source & barrier

(Image source: http://upload.wikimedia.org/wikipedia/commons/a/af/Simple_ripple_tank.svg)

Example for the detector:

A screen

Aerial / microwave probe

A strobe / lamp

What is observed (wave patterns are observed on the viewing screen)                                 

(ii)

(Image source: http://tap.iop.org/vibration/progressive/311/img_full_46672.gif)

For apparatus, e.g. loudspeaker, and slit / edge

For detector, e.g. microphone & c.r.o / ear

What is observed (as the microphone is moved away / towards the loudspeaker, the amplitude of the wave on the cro changes)

Question 242: [Units]

M = kv^p ρ^q g^r

Find the value of p, where M = mass, v = velocity, ρ = density, g = acceleration due to gravity, given that k, p, q and r are dimensionless scalars.



Solution 242:
Unit of mass M: kg
Units of velocity v: ms^-1

Density = mass / volume
Units of density ρ: kg m^-3

Units of acceleration due to gravity g: ms^-2

For the equation to be homogeneous, the overall units on the right-hand side should be equal to the unit on the left-hand side (kg).

M = kv^p ρ^q g^r

On the right-hand side,
[v^p ρ^q g^r] = (ms^-1)^p (kgm^-3)^q (ms^-2)^r 
{Expand the exponents of the units}
[v^p ρ^q g^r] = (m^ps^-p) (kg^qm^-3q) (m^rs^-2r)
{Group the exponents of each unit together}
[v^p ρ^q g^r] = (m^p-3q+r) (s^-p-2r) (kg^q)

Since the exponent of the unit ‘kg’ is 1 on the left-hand side, q = 1

[v^p ρ^q g^r] = (m^p-3+r) (s^-p-2r) (kg¹)

Additionally, there is no units of ‘m’ and ‘s’ on the left-hand side. Therefore, the overall exponents of ‘m’ and ‘s’ should be zero.
For ‘m’: p – 3 + r = 0              ………………….. (1)
For ‘s’: -p – 2r = 0                    ………………….. (2)

From equation (2)
p = 2r

Substitute p = 2r in equation (1)
2r – 3 + r = 0   giving r = 1

So, p = 2r = 2(1) = 2









Question 243: [Forces > Equilibrium]

(a) Explain what is meant by centre of gravity.

(b) Define the moment of a force.

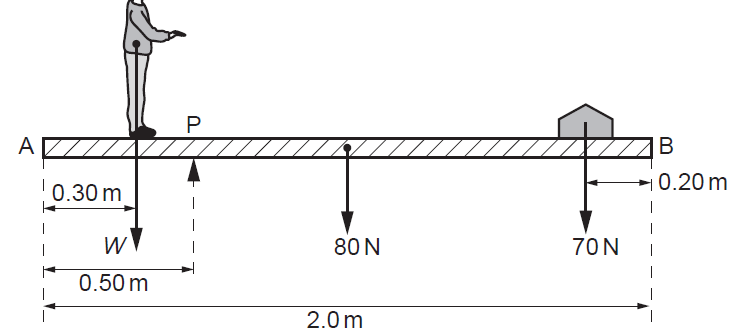
(c) Student is being weighed. Student, of weight W, stands 0.30 m from end A of uniform plank AB, as shown in Fig.

Plank has weight 80 N and length 2.0 m. A pivot P supports plank and is 0.50 m from end A.

Weight of 70 N is moved to balance weight of the student. Plank is in equilibrium when weight is 0.20 m from end B.

(i) State the two conditions necessary for plank to be in equilibrium.

(ii) Determine weight W of the student.

(iii) If only the 70 N weight is moved, there is a maximum weight of student that can be determined using arrangement shown in Fig. State and explain one change that can be made to increase this maximum weight.

Reference: Past Exam Paper – June 2011 Paper 21 Q3



Solution 243:

(a) The centre of gravity is the point where the weight of an object / gravitational force may be considered to act

(b) The moment of a force is the product of the force and the perpendicular distance (to the pivot).

(c)

(i)

The sum / net / resultant force is zero.

The net / resultant moment is zero. OR Sum of clockwise moments = sum of anticlockwise moments

(ii)

{For equilibrium, sum of anticlockwise moments = sum of clockwise moments. Weight W of student is at (0.50 – 0.30 =) 0.20m to the pivot. Weight (due to centre of gravity) of plank is at (1.00 – 0.50=) 0.50m to pivot. The 70N weight is at (2.00 – 0.20 – 0.50 =) 1.30m to pivot.}

W x (0.50 – 0.30) = 80(0.5) + 70(1.3)

0.2W = 40 + 91

Weight W of student = 655N

(iii)

{When the 70N weight is moved furthest possible from the pivot (that is, it is at end B), it causes a maximum moment. Since the questions says that if only the 70N weight is moved, there will be a maximum weight of the student (who is stationary) for which equilibrium can be achieved. The question asks for a way to increase this maximum possible weight W of student.}

EITHER

{One of the conditions for equilibrium is that sum of clockwise moments = sum of anticlockwise moments. By increasing the clockwise moment caused by the 70N, a greater weight would be required for equilibrium.}

Moving the pivot to the left gives a greater clockwise moment (distance of 70N weight to pivot increases) / smaller anticlockwise moment (So, a greater maximum weight is required to cause an anticlockwise moment equal in magnitude to the clockwise moment)

OR

{Additionally, as defined previously, moment is the product of force and the perpendicular distance to the pivot. So, if we want to increase the weight, we need to decrease the distance from the pivot.}

Moving the weight W to the left (distance of weight W to pivot decreases) gives a smaller anticlockwise moment (So, a greater maximum weight is required to cause an anticlockwise moment equal in magnitude to the clockwise moment)

Question 244: [Dynamics > Newton’s Laws of Motion]
(a) Distinguish between the mass and the weight of a body. State the unit in which each is measured.                                                                              [4]

(b) Show that
(i) the base units of the acceleration of free fall are the same as the base units of gravitational field strength,
(ii) the newton second is a unit of momentum                       [4]

(c) In the United States, planes are under consideration for launching a satellite by use of a space gun. The satellite, of mass 2000kg, accelerates uniformly along a tube of length 1200m and reaches a speed of 8000ms^-1.
Calculate
(i) the momentum of the satellite as it leaves the tube
(ii) the time it takes to accelerate along the tube
(iii) the force causing the acceleration
(iv) the acceleration                                                     [8]

(d)
(i) It would be impossible to use the space gun in (c) for manned space flights. Suggest a reason.
(ii) It would be an advantage to site the gun on the Earth’s equator pointing eastwards. Suggest a reason.                                                            [4]

Reference: Past Exam Paper – N92 / III / 1



Solution 244:

(a)

The mass is the property of a body resisting changes in motion / mass is the quantity of matter in a body / measure of the inertia to changes in motion. Unit of mass: kilogram (kg).

The weight of a body is the force acting on the body due to the gravitational field / the force due to gravity OR gravitational force. Unit of weight: newton (N).

(b)

(i)

Units of acceleration of free fall = ms^-2

The gravitational field strength at a point is defined as the gravitational force acting on a body of unit mass at that point.

Gravitational field strength = (Gravitational) Force / Mass
Units of gravitational field strength = [Force] / [Mass] = [kg ms^-2] / [kg] = ms^-2

(ii)
Momentum = Mass x Velocity
Units of momentum = kg ms^-1

Newton is the unit of force. [Force = Mass x Acceleration]
Newton in SI units = kg ms^-2  

Units of momentum can be re-written as
Units of momentum = [kg ms^-2] s¹ = Ns

(c)
(i)
Mass, m = 2000kg
Velocity, v at the end of the tube = 8000ms^-1
Momentum, p of satellite = mv = 2000 (8000) = 1.6x10⁷kgms^-1

(ii)
Average speed = Total distance / Total time
Average speed = (u + v) / 2 = (0 + 8000) / 2 = 4000ms^-1
Time, t = Distance / Speed = 1200 / 4000 = 0.30s

(iii)
Force = Δp / t = (1.6x10⁷) / 0.3 = 53.3x10⁶N = 53.3MN

(iv)
Force = Mass x Acceleration
Acceleration = Force / Mass = (53.3x10⁶) / 2000 = 2.67x10⁴ms^-2

(d)
(i)
From (c)(iii), it can be seen that the force acting on the satellite is very large. If a man is present on the satellite, this force will also act on him. So, it is not safe.

(ii)
To orbit the Earth, an object needs to reach a certain velocity.
The Earth rotates about its own axis, with the direction of rotation being from west to east (eastwards).
The circumference (at the equator) of Earth is about 40075km. The Earth also rotates around the Sun with a period of rotation being 24 hours. So, the speed of rotation of the Earth is about (40075km / 24hr =) 465ms^-1. The speed of Earth’s rotation is highest at the Equator and changes as we go North or South away from the equator.
So, at the surface of the Earth’s equator, a point travels at a speed of 465ms^-1 eastwards. Therefore, by siting the gun on the Earth’s equator pointing eastwards, the satellite also has an initial speed of 465ms^-1. Less force would be required to cause it to accelerate until it reaches the orbit velocity.