Linear Algebra: #6 Linear Mappings and Matrices
Now, the most obvious problem with our previous notation for vectors was that the lists of the coordinates (x1, . . . , xn) run over the page, leaving hardly any room left over to describe symbolically what we want to do with the vector. The solution to this problem is to write vectors not as horizontal lists, but rather as vertical lists. We say that the horizontal lists are row vectors, and the vertical lists are column vectors. This is a great improvement! So whereas before, we wrote
v = (x1, . . . , xn),
now we will write
It is true that we use up lots of vertical space on the page in this way, but since
the rest of the writing is horizontal, we can afford to waste this vertical space. In
addition, we have a very nice system for writing down the coordinates of the vectors
after they have been mapped by a linear mapping.
To illustrate this system, consider the rotation of the plane through the angle φ, which was described in the last section. In terms of row vectors, we have (x1, x2) being rotated into the new vector(x1 cos φ − x2 sin φ, x1 sin φ + x2 cos φ). But if we change into the column vector notation, we have
That is, matrix multiplication gives the result of the linear mapping.
Expressing f : V → W in terms of bases for both V and W To illustrate this system, consider the rotation of the plane through the angle φ, which was described in the last section. In terms of row vectors, we have (x1, x2) being rotated into the new vector(x1 cos φ − x2 sin φ, x1 sin φ + x2 cos φ). But if we change into the column vector notation, we have
A · v = f(v)
That is, matrix multiplication gives the result of the linear mapping.
The example we have been thinking about up till now (a rotation of ℜ2) is a linear mapping of ℜ2 into itself. More generally, we have linear mappings from a vector space V to a different vector space W (although, of course, both V and W are vector spaces over the same field F).
So let {v1, . . . , vn} be a basis for V and let {w1, . . . , wm} be a basis for W. Finally, let f : V → W be a linear mapping. An arbitrary vector v ∈ V can be expressed in terms of the basis for V as
The question is now, what is f(v)? As we have seen, f(v) can be expressed in terms of the images f(vj) of the basis vectors of V. Namely
But then, each of these vectors f(vj) in W can be expressed in terms of the basis vectors in W, say
for appropriate choices of the “numbers” cij ∈ F. Therefore, putting this all together, we have
In the matrix notation, using column vectors relative to the two bases {v1, . . . , vn} and {w1, . . . , wm}, we can write this as
When looking at this m×n matrix which represents the linear mapping f : V → W, we can imagine that the matrix consists of n columns. The i-th column is then
That is, it represents a vector in W, namely the vector vi = c1iw1+ · · · + cmiwm.
But what is this vector ui? In the matrix notation, we have
where the single non-zero element of this column matrix is a 1 in the i-th position from the top. But then we have
Two linear mappings, one after the other
Things become more interesting when we think about the following situation. Let V, W and X be vector spaces over a common field F. Assume that f : V → W and g : W → X are linear. Then the composition f ◦ g : V → X, given by
f ◦ g(v) = g(f(v))
for all v ∈ V is clearly a linear mapping. One can write this as
Let {v1, . . . , vn} be a basis for V, {w1, . . . , wm} be a basis for W, and {x1, . . . , xr} be a basis for X. Assume that the linear mapping f is given by the matrix
and the linear mapping g is given by the matrix
There are so many summations here! How can we keep track of everything? The answer is to use the matrix notation. The composition of linear mappings is then simply represented by matrix multiplication. That is, if
then we have
So this is the reason we have defined matrix multiplication in this way. Recall that if A is an m x n matrix and B is an r x m matrix, then the product BA is an r x n matrix whose kj-th element is the summation of dkicij with i from 1 to m.


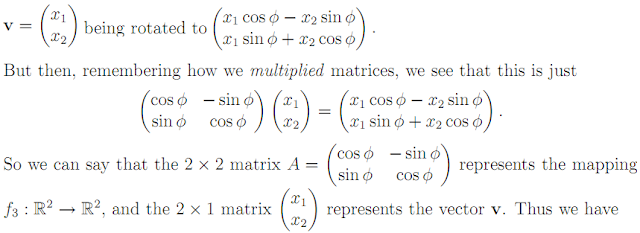














No comments:
Post a Comment
If it's a past exam question, do not include links to the paper. Only the reference.
Comments will only be published after moderation