Complex Analysis: #30 Jensen`s Formula
Theorem 51 (Jensen’s Inequality)
Let R > 0 be given and let the (non-constant) analytic function f be defined in a region containing the closed disc DR = {z ∈ ℂ : |z| ≤ R}. Assume f(0) ≠ 0 and also f(z) ≠ 0 for all z with |z| = R. Let the zeros of f in DR be z1, . . ., zn . (Here a zero is listed m times if it is a zero of order m.) We assume the zeros are ordered according to their increasing absolute value. Let ||f||R = max{|f(z)| : |z| = R}. Then we have
More generally, thinking about various values of R, let vf(R) = n be the number of zeros of f in DR, where R, thus n, is allowed to vary. Then we have Jensen’ inequality:
It is obviously analytic in DR. Furthermore, we have |g(z)| = |f(z)| when |z| = R. This implies that |g(w)| ≤ ||f||R for all w ∈ DR. [If we had a point w∗ in the interior of DR with |g(w∗)| > ||f||R, then we can assume that it is maximal with respect to this property. However, that would contradict theorem 19.] Therefore
Theorem 52 (Jensen’s Formula)
The same assumptions as in the previous theorem. Then we have
Proof
In this proof, we will first look at two very simple cases:
1. We first prove Jensen’s formula in the simple case that there are no zeros of f in DR. Then again, as in exercise 12.1, we have an analytic function g, defined in a neighborhood of DR, with f = eg. Or put another way, g = log f. (To be definite, we could specify that log f(0) should be in the principle branch of the logarithm.) Then Cauchy’s formula is simply
which establishes the theorem in the first case.
2. The second case is even simpler. Namely, let ζ be a complex number with |ζ| < R. That is, ζ is some point in the interior of DR. This second case is that the function f is simply f(z) = z − ζ. We then define a new function, namely





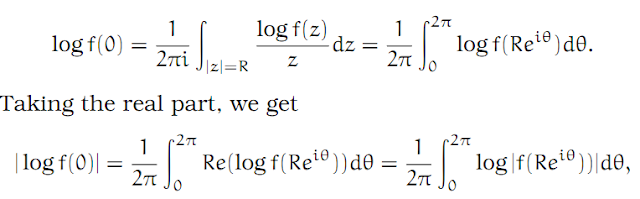

Please show the related Mittag-Leffler approach.
ReplyDeleteIt's been some time since I went through this. So, I don't think I'll be updating these sections.
DeleteSorry. Try to find it on the web.