Plane Harmonic Wave Equations in Harmonic Isotropic Linear Stationary (HILS) medium
The general Maxwell`s equations are
For linearity and isotropy, we have
We will use the following identity to obtain the wave equations
To derive the wave equation for E
replacing Jfree in the equation (7)
So, we get the wave equation for E
To obtain the wave equation for B in Harmonic Isotropic Linear Stationary (HILS) medium, we follow the same principle.
Taking the divergence of B =0 (Maxwell second equation above) and writing B in terms of H as appropriate for linearity and isotropy, we obtain
From equation (4) of the Maxwell`s equations, we obtain equation (12) below, and upon simplifying and applying curl on both sides, we obtain the following form of the equation
Then, we replace the right-hand side of equation (11) and the curl of E (from the 3rd Maxwell`s equation) in equation (12)
Hence, we have obtain the wave equation for H in a HILS medium.
So, we have finally obtained the wave equations for both E and H. That`s what we wanted.
Now, let`s try an additional simplification for the wave equation for E.
let E be in the x-direction,
We can therefore replace the right-hand side of equation (9) with the result of the above equation
Equation (15) is the solution for Ex that would be obtained from (14).
As E and H are transverse, an example of a solution would be
where Z is the characteristic impedance.



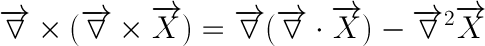





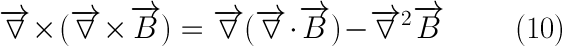

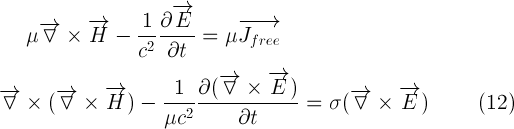





No comments:
Post a Comment
If it's a past exam question, do not include links to the paper. Only the reference.
Comments will only be published after moderation