Linear Algebra: #4 Linear Independence and Dimension
Let v1, . . . , vn ∈ V be finitely many vectors in the vector space V over the field F. We say that the vectors are linearly dependent if there exists an equation of the form
a1· v1 + · · · + an· vn = 0,
This definition is undoubtedly the most important idea that there is in the theory of linear algebra!
Examples
- In ℜ2 let v1 = (1, 0), v2 = (0, 1) and v3 = (1, 1). Then the set {v1, v2, v3} is linearly dependent, since we have
v1 + v2 - v1 = 0
On the other hand, the set {v1, v2} is linearly independent. - In C0([0, 1], ℜ), let f1 : [0, 1] → ℜ be given by f1(x) = 1 for all x ∈ [0, 1]. Similarly, let f2 be given by f2(x) = x, and f3 is f3(x) = 1 − x. Then the set {f1, f2, f3} is linearly dependent.
Now take some vector space V over a field F, and let S ⊂ V be some subset of V. (The set S can be finite or infinite here, although we will usually be dealing with finite sets.) Let v1, . . . , vn ⊂ S be some finite collection of vectors in S, and let a1, . . . , an∈ F be some arbitrary collection of elements of the field. Then the sum
a1· v1 + · · · + an· vn
is a linear combination of the vectors v1, . . . , vn in S. The set of all possible linear combinations of vectors in S is denoted by span(S), and it is called the linear span of S. One also writes [S]. S is the generating set of [S]. Therefore if [S] = V, then we say that S is a generating set for V . If S is finite, and it generates V, then we say that the vector space V is finitely generated.
Theorem 5
Given S ⊂ V, then [S] is a subspace of V.
Proof
A simple consequence of theorem 2.
Examples
- For any n ∈ ℕ, let
Then S = {e1, e2 ,. . . , en} is a generating set for ℜn
- On the other hand, the vector space C0([0, 1], ℜ) is clearly not finitely generated. (In general such function spaces — which play a big role in quantum field theory, and which are studied using the mathematical theory of functional analysis — are not finitely generated. However in this lecture, we will mostly be concerned with finitely generated vector spaces. )
So let S = {v1, . . . , vn} ⊂ V be a finite set. From now on in these discussions, we will assume that such sets are finite unless stated otherwise.
Theorem 6
Let w = a1v1 + · · · + anvn be some vector in [S] ⊂ V, where a1, . . . , an are arbitrarily given elements of the field F. We will say that this representation of w is unique if, given some other linear combination, w = b1v1 + · · · + bnvn , then we must have bi = ai for all i = 1, . . . , n. Given this, then we have that the set S is linearly independent ⇔ the representation of all vectors in the span of S as linear combinations of vectors in S is unique.
Proof.
‘⇐’ We certainly have 0v1 + · · · + 0vn= 0. Since this representation of the zero vector is unique, it follows S is linearly independent.
‘⇒’ Can it be that S is linearly independent, and yet there exists a vector in the span of S which is not uniquely represented as a linear combination of the vectors in S? Assume that there exist elements a1, . . . , an and b1, . . . , bn of the field F, where aj ≠ bj , for at least one j between 1 and n, such that
shows that S cannot be a linearly independent set.
Definition
Assume that S ⊂ V is a finite, linearly independent subset with [S] = V. Then S is called a basis for V.
Lemma
Assume that S = {v1, . . . , vn} ⊂ V is linearly dependent. Then there exists some j ∈ {1, . . . , n}, and elements ai ∈ F, for i ≠ j, such that
Proof
Since S is linearly dependent, there exists some non-trivial linear combination of the elements of S, summing to the zero vector,
such that bj ≠ 0, for at least one of the j. Take such a one. Then

Corollary
Let S = {v1, . . . , vn} ⊂ V be linearly dependent, and let vj be as in the lemma above. Let S' = {v1, . . . , vj-1 ,vj+1 , . . . ,vn} be S, with the element vj removed.
Theorem 7
Assume that the vector space V is finitely generated. Then there exists a basis for V.
Proof
Since V is finitely generated, there exists a finite generating set. Let S be such a finite generating set which has as few elements as possible. If S were linearly dependent, then we could remove some element, as in the lemma, leaving us with a still smaller generating set for V. This is a contradiction. Therefore S must be a basis for V.
Theorem 8
Let S = {v1, . . . , vn} be a basis for the vector space V, and take some arbitrary non-zero vector w ∈ V. Then there exists some j ∈ {1, . . . , n}, such that
S'
= {v1, . . . , vj-1 , w, vj+1 , . . . ,vn}
is also a basis of V.
Proof
Writing w = a1v1 + · · · + anvn, we see that since w ≠ 0, at least one aj ≠ 0. Taking that j, we write
We now prove that [S'] = V. For this, let u ∈ V be an arbitrary vector. Since S is a basis for V, there exists a linear combination u = b1v1 + · · · + bnvn. Then we have
This shows that [S'] = V.
In order to show that S' is linearly independent, assume that we have
for some c, and ci ∈ F. Since the original set S was assumed to be linearly independent, we must have cai + ci = 0, for all i. In particular, since cj = 0, we have caj = 0. But the assumption was that aj ≠ 0. Therefore we must conclude that c = 0. It follows that also ci = 0. , for all i ≠ j. Therefore, S' must be linearly independent.
Theorem 9 (Steinitz Exchange Theorem)
Let S = {v1, . . . , vn} be a basis of V and let T = {w1, . . . , wm} ⊂ V be some linearly independent set of vectors in V. Then we have m ≤ n. By possibly re-ordering the elements of S, we may arrange things so that the set
U = {w1, . . . , wm , vm+1 , . . . ,vn}
is a basis for V.
Proof
Use induction over the number m. If m = 0 then U = S and there is nothing to prove.
Therefore assume m ≥ 1 and furthermore, the theorem is true for the case m − 1. So consider the linearly independent set T' = {w1, . . . , wm-1}. After an appropriate re-ordering of S, we have U' = {w1, . . . , wm-1, vm , . . . ,vn} being a basis for V. Note that if we were to have n < m, then T' would itself be a basis for V. Thus we could express wm as a linear combination of the vectors in T'. That would imply that T was not linearly independent, contradicting our assumption. Therefore, m ≤ n.
Now since U' is a basis for V, we can express wmas a linear combination
wm = a1w1 + · · · + am-1wm-1 + amvm + · · · + anvn
If we had all the coefficients of the vectors from S being zero, namely
am = am+1 = · · · = an = 0,
then we would have wm being expressed as a linear combination of the other vectors in T. Therefore T would be linearly dependent, which is not true. Thus one of the aj ≠ 0, for j ≥ m. Using theorem 8, we may exchange wm for the vector vj in U', thus giving us the basis U.
Theorem 10 (Extension Theorem)
Assume that the vector space V is finitely generated and that we have a linearly independent subset S ⊂ V. Then there exists a basis B of V with S ⊂ B.
Proof
If [S] = V then we simply take B = S. Otherwise, start with some given basis A ⊂ V and apply theorem 9 successively.
Theorem 11
Let U be a subspace of the (finitely generated) vector space V. Then U is also finitely generated, and each possible basis for U has no more elements than any basis for V.
Proof
Assume there is a basis B of V containing n vectors. Then, according to theorem 9, there cannot exist more than n linearly independent vectors in U. Therefore U must be finitely generated, such that any basis for U has at most n elements.
Theorem 12
Assume the vector space V has a basis consisting of n elements. Then every basis of V also has precisely n elements.
Proof
This follows directly from theorem 11, since any basis generates V, which is a subspace of itself.
Definition
The number of vectors in a basis of the vector space V is called the dimension of V, written dim(V).
Definition
Let V be a vector space with subspaces X, Y ⊂ V. The subspace X + Y = [X ∪ Y ] is called the sum of X and Y. If X ∩ Y = {0}, then it is the direct sum, written X ⊕ Y.
Theorem 13 (A Dimension Formula)
Let V be a finite dimensional vector space with subspaces X, Y ⊂ V. Then we have
dim(X + Y) = dim(X) + dim(Y) − dim(X ∩ Y).
Corollary
dim(X ⊕ Y) = dim(X) + dim(Y).
Proof of Theorem 13
Let S = {v1, . . . , vn} be a basis of X ∩ Y. According to theorem 10, there exist extensions T = {x1, . . . , xm} and U = {y1, . . . , yr}, such that S ∪ T is a basis for X and S ∪ U is a basis for Y. We will now show that, in fact, S ∪ T ∪ U is a basis for X + Y.
To begin with, it is clear that X+Y = [S ∪T ∪U]. Is the set S ∪T ∪U linearly independent? Let
Then we have y = −v − x. Thus y ∈ X. But clearly we also have, y ∈ Y. Therefore y ∈ X ∩ Y. Thus y can be expressed as a linear combination of vectors in S alone, and since S ∪ U is is a basis for Y , we must have ck = 0 for k = 1, . . . , r. Similarly, looking at the vector x and applying the same argument, we conclude that all the bj are zero. But then all the ai must also be zero since the set S is linearly independent.
Putting this all together, we see that the dim(X) = n +m, dim(Y) = n +r and dim(X ∩ Y) = n. This gives the dimension formula.
Theorem 14
Let V be a finite dimensional vector space, and let X ⊂ V be a subspace. Then there exists another subspace Y ⊂ V, such that V = X ⊕ Y.
Proof
Take a basis S of X. If [S] = V then we are finished. Otherwise, use the extension theorem (theorem 10) to find a basis B of V, with S ⊂ B. Then Y = [B \ S] satisfies the condition of the theorem. (The notation B \ S denotes the set of elements of B which are not in S)

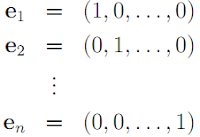







No comments:
Post a Comment
If it's a past exam question, do not include links to the paper. Only the reference.
Comments will only be published after moderation